Предмет: Геометрия,
автор: lnet213
Решите пожалуйста 174 пример, очень нужно
Приложения:
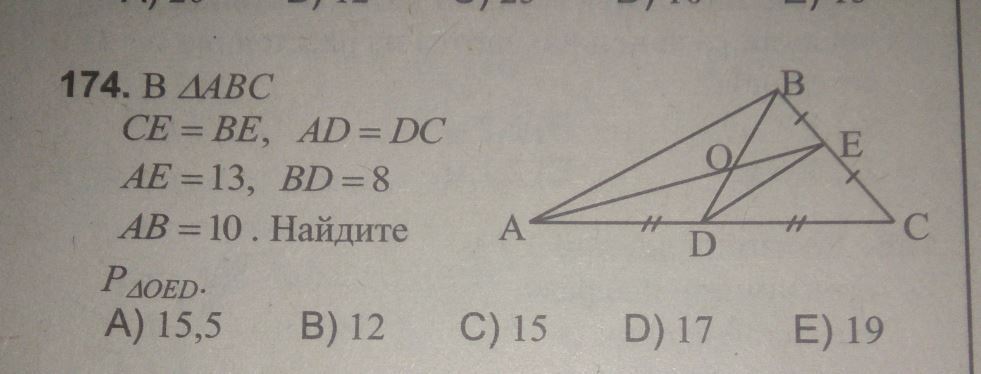
Ответы
Автор ответа:
0
ДЕ - средняя линия. ДЕ=АВ/2=5.
Тр-ки АОВ и ДОЕ подобны т.к. ∠АОВ=∠ДОЕ, ∠ВАО=∠ДЕО (АВ║ДЕ и АЕ - секущая).
Коэффициент подобия тр-ков АОВ и ДОЕ: k=ДЕ/АВ=1:2.
ЕО=2АО ⇒ ЕО=АЕ/3=13/3,
ДО=2ВО ⇒ ДО=ВД/3=83,
Р(ОЕД)=ЕО+ДО+ДЕ=5+(13+8)/3=12 - это ответ.
Тр-ки АОВ и ДОЕ подобны т.к. ∠АОВ=∠ДОЕ, ∠ВАО=∠ДЕО (АВ║ДЕ и АЕ - секущая).
Коэффициент подобия тр-ков АОВ и ДОЕ: k=ДЕ/АВ=1:2.
ЕО=2АО ⇒ ЕО=АЕ/3=13/3,
ДО=2ВО ⇒ ДО=ВД/3=83,
Р(ОЕД)=ЕО+ДО+ДЕ=5+(13+8)/3=12 - это ответ.
Автор ответа:
0
DE - средняя линия

Треугольники AOB и DOE подобны, т.к. ∠AOB=∠DOE,
∠BAO=∠DEO, AB║DE и AE - это секущая
Коэффициент подобия треугольников AOB и DOE:
EO=2AO ⇒ ,
,
DO=2BO ⇒ ,
,

Ответ: 12
Треугольники AOB и DOE подобны, т.к. ∠AOB=∠DOE,
∠BAO=∠DEO, AB║DE и AE - это секущая
Коэффициент подобия треугольников AOB и DOE:
EO=2AO ⇒
DO=2BO ⇒
Ответ: 12
Похожие вопросы
Предмет: Математика,
автор: azarbaani07
Предмет: Русский язык,
автор: beehjj6
Предмет: Українська мова,
автор: Аноним
Предмет: Математика,
автор: lidusik1997
Предмет: Биология,
автор: stepanmorozov