Предмет: Алгебра,
автор: lordphantom
РЕШИТЕ НЕРАВЕНСТВО, УМОЛЯЮ)))
Приложения:
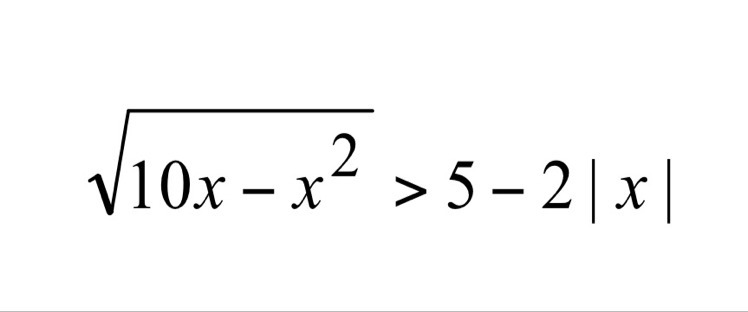
Ответы
Автор ответа:
0
ОДЗ:
выражение под корнем должно быть неотрицательное:
10x-x²≥0
x*(10-x)≥0
решая методом интервалов получаем:
x∈[0;10]
т.к. х может принимать только неотрицательные значения(иначе неравенство не имеет смысла), то модуль раскрываем с +.

Смотрим рисунок.
далее стоит рассмотреть два случая.
a)Когда выражение справа меньше нуля
5-2x<0
x>2.5
тогда решением будет ОДЗ неравенства, то есть x∈[0;10]
итого: x∈(2.5;10]
б)когда выражение справа >=0
5-2x≥0
x≤2.5
тогда возведём обе части неравенства в квадрат:

решая методом интервалов получаем:
x∈(1;5)
итого x∈(1;2,5)
объединяя эти два ответа получаем x∈(1;10]
ответ: x∈(1;10]
выражение под корнем должно быть неотрицательное:
10x-x²≥0
x*(10-x)≥0
решая методом интервалов получаем:
x∈[0;10]
т.к. х может принимать только неотрицательные значения(иначе неравенство не имеет смысла), то модуль раскрываем с +.
Смотрим рисунок.
далее стоит рассмотреть два случая.
a)Когда выражение справа меньше нуля
5-2x<0
x>2.5
тогда решением будет ОДЗ неравенства, то есть x∈[0;10]
итого: x∈(2.5;10]
б)когда выражение справа >=0
5-2x≥0
x≤2.5
тогда возведём обе части неравенства в квадрат:
решая методом интервалов получаем:
x∈(1;5)
итого x∈(1;2,5)
объединяя эти два ответа получаем x∈(1;10]
ответ: x∈(1;10]
Приложения:
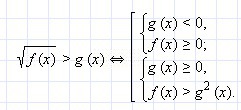
Похожие вопросы
Предмет: Алгебра,
автор: katya18200406
Предмет: Литература,
автор: Kirilltop22847
Предмет: Химия,
автор: Аноним
Предмет: Физика,
автор: sarinasharapov
Предмет: Математика,
автор: kirill2002ghetto