Предмет: Алгебра,
автор: cdsme
Вычислите двойной интеграл
Приложения:
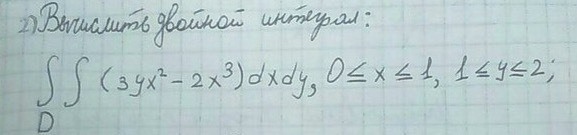
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Биология,
автор: Spallmen
Предмет: Русский язык,
автор: lubaxa11
Предмет: Физика,
автор: olyapaw30
Предмет: Алгебра,
автор: Amur1tigerr
Предмет: Алгебра,
автор: akerke73