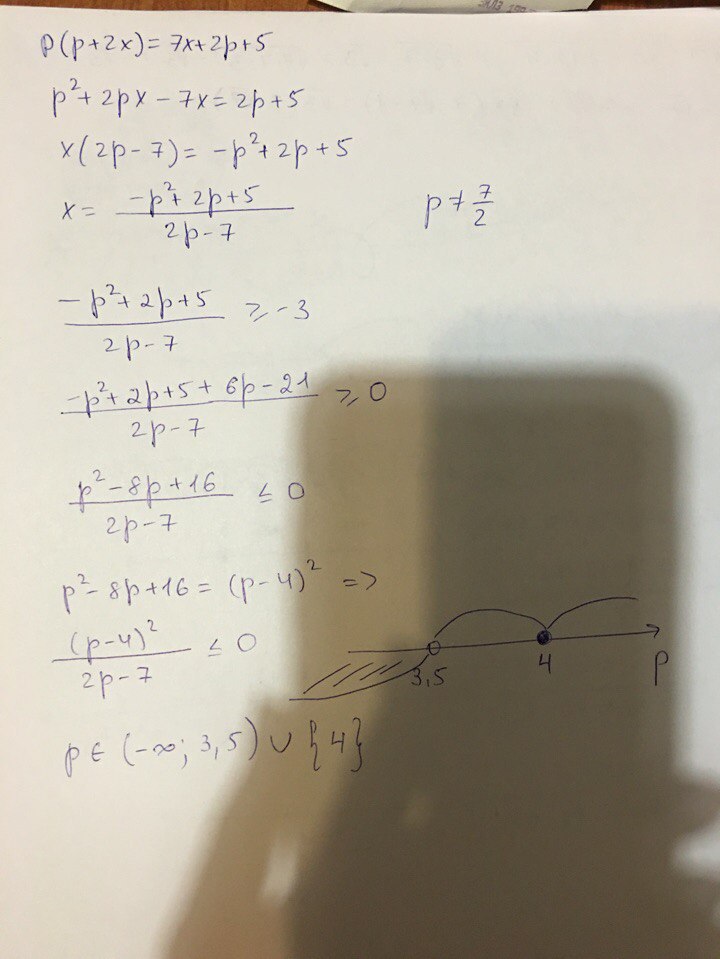Question

Помогите, пожалуйста, решить уравнение с параметром!!!
Найти множество значений p, для которых корень уравнения p(p + 2x) = 7x + 2p + 5 больше либо равен -3.

Answer 1

р^2+2px-7x=2p+5

2px-7x=2p+5-p^2

x(2p-7)=2p+5-p^2

x=(2p+5-p^2)/(2p-7)

по условию корень должен быть больше или равен -3

(2p+5-p^2)/(2p-7) больше или равно -3

(2p+5-p^2+3(2p-7))/(2p-7) больше или равно 0

(2p+5-p^2+6p-21)/(2p-7) больше или равно 0

это выполнимо, когда числитель больше или равен 0 и знаменатель больше 0 или если числитель меньше или равен 0 и знаменатель меньше 0

-p^2+8p-16=0

D=64-64=0

1.                                                    или 2.

-(p-4)^2 больше или равно 0,             -(p-4)^2  меньше или равно 0,

2p-7 больше 0                                      2p-7 меньше 0

1.

-(p-4)^2 всегда меньше или равно 0,

значит нам подходит только p=4 , при этом 2p-7 больше 0, значит p=4 является решением

2.

-(p-4)^2 меньше или равно 0 - всегда

2p-7 меньше 0

2p меньше 7

p меньше 3,5

Таким образом, ответом будет промежуток от минус бесконечности до 3,5 (исключая конец) и ещё 4.

Answer 2

Решение на фотографии