Question

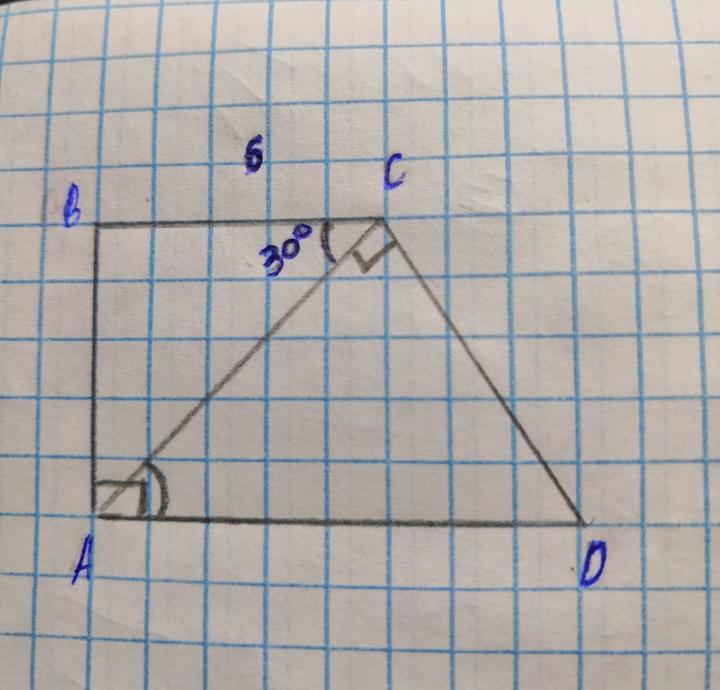
В трапеции ABCD основание AD перпендикулярно боковой стороне AB, диагональ AC перпендикулярна стороне CD. Найдите длину стороны CD, если BC=6см,
угол BCA=30 градусов.

Answer 1

Дано: ABCD - прямоугольная трапеция(т.к. AB ⊥ AD)

AC ⊥ CD

BC = 6 см.

∠BCA = 30°

Найти: CD

Рассмотрим ΔABC - прямоугольный

$cosangle BCA = frac{BC}{AC}\\cosangle BCA = cos 30^circ = frac{sqrt3}{2}\\frac{sqrt3}{2} = frac{6}{AC}\\AC = frac{12}{sqrt3} = 4sqrt3; cm.$

Рассмотрим ΔACD - прямоугольный

AC ║ BC - по определению трапеции, AC - секущая ⇒ ∠BCA = ∠CAB = 30° (накрест лежащие углы при параллельных прямых равны)

$text{tg}angle CAD = frac{CD}{AC}\\text{tg}30^circ = frac{sqrt3}{3}\\frac{sqrt3}{3} = frac{CD}{4sqrt3}\\CD = frac{4sqrt3cdotsqrt3}{3} = 4; cm.$

Ответ: 4 см