Предмет: Алгебра,
автор: Nikitasupamida
решите пожалуйста,срочно !
Приложения:
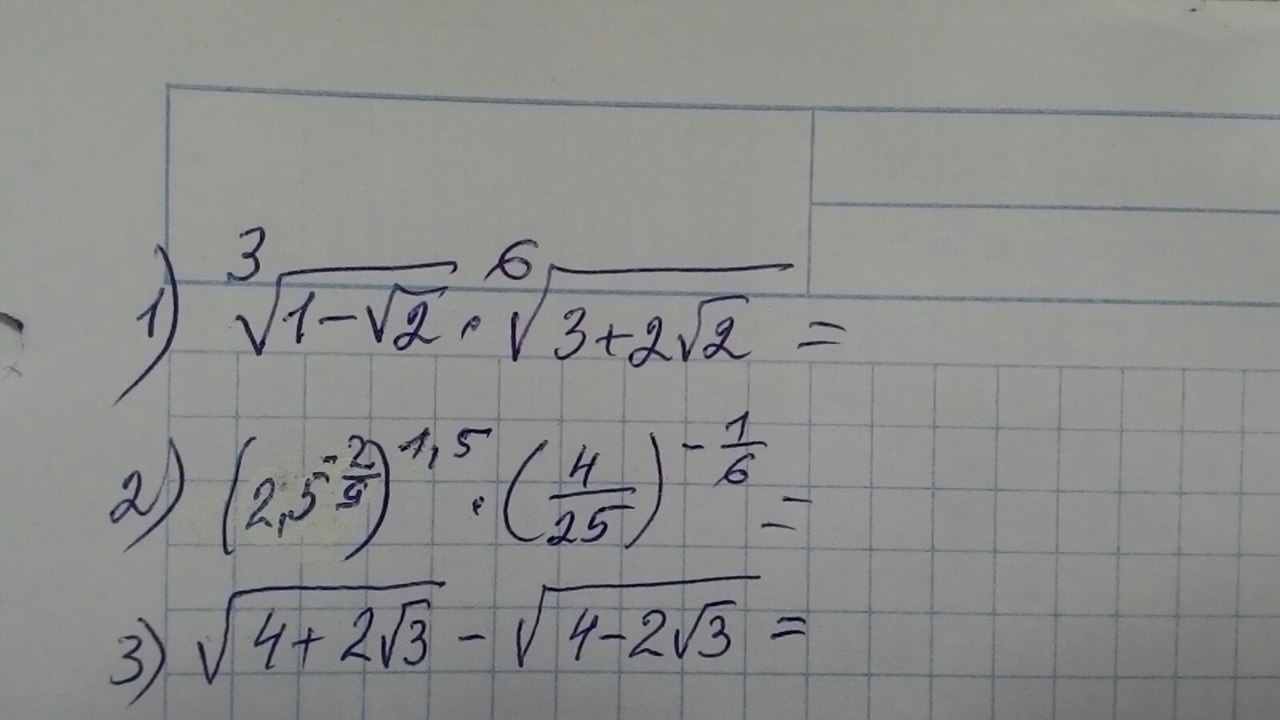
Ответы
Автор ответа:
0
1)
![sqrt[3]{1- sqrt{2} } sqrt[6]{3+ 2sqrt{2} }=sqrt[6]{(1- sqrt{2})^2(3+ 2sqrt{2}) }= \ =sqrt[6]{(1- 2sqrt{2}+2)(3+ 2sqrt{2})}=sqrt[6]{(3- 2sqrt{2})(3+ 2sqrt{2})}= \ =sqrt[6]{9- 4*2}= sqrt[6]{1}=1 sqrt[3]{1- sqrt{2} } sqrt[6]{3+ 2sqrt{2} }=sqrt[6]{(1- sqrt{2})^2(3+ 2sqrt{2}) }= \ =sqrt[6]{(1- 2sqrt{2}+2)(3+ 2sqrt{2})}=sqrt[6]{(3- 2sqrt{2})(3+ 2sqrt{2})}= \ =sqrt[6]{9- 4*2}= sqrt[6]{1}=1](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B1-+sqrt%7B2%7D+%7D+sqrt%5B6%5D%7B3%2B+2sqrt%7B2%7D+%7D%3Dsqrt%5B6%5D%7B%281-+sqrt%7B2%7D%29%5E2%283%2B+2sqrt%7B2%7D%29+%7D%3D+%5C+%3Dsqrt%5B6%5D%7B%281-+2sqrt%7B2%7D%2B2%29%283%2B+2sqrt%7B2%7D%29%7D%3Dsqrt%5B6%5D%7B%283-+2sqrt%7B2%7D%29%283%2B+2sqrt%7B2%7D%29%7D%3D+%5C+%3Dsqrt%5B6%5D%7B9-+4%2A2%7D%3D+sqrt%5B6%5D%7B1%7D%3D1)
2)

3)

2)
3)
Похожие вопросы
Предмет: История,
автор: DrakeOml
Предмет: Алгебра,
автор: swdawsew
Предмет: Алгебра,
автор: sarokinsergej30
Предмет: Математика,
автор: попро
Предмет: Литература,
автор: delitol10