Предмет: Алгебра,
автор: dbnfkbr0079
Найти уравнение касательной к графику функции в точке с обсцисой х0
Y=sinx,x0=pi/3
Ответы
Автор ответа:
0
y=sinx
y(π/3)=sinπ/3=√3/2
y'=cosx
y'(π/3)=cosπ/3=1/2
y=√3/2 + 1/2 (x- π/3)=√3/2 + ¹/₂ x - (π/6)= 0.5x + √3/2 - π/6
y= 0.5x + √3/2 - π/6 - уравнение касательной.
y(π/3)=sinπ/3=√3/2
y'=cosx
y'(π/3)=cosπ/3=1/2
y=√3/2 + 1/2 (x- π/3)=√3/2 + ¹/₂ x - (π/6)= 0.5x + √3/2 - π/6
y= 0.5x + √3/2 - π/6 - уравнение касательной.
Автор ответа:
0
см. вложение
\\\\\\\\\
\\\\\\\\\
Приложения:
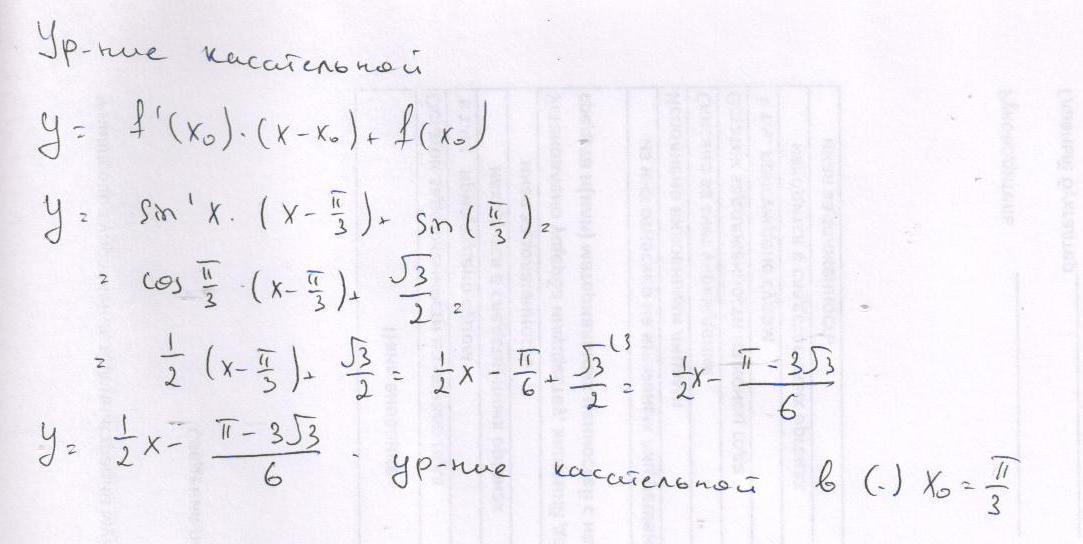
Похожие вопросы
Предмет: Математика,
автор: gulsaranurpeisova
Предмет: Математика,
автор: FlickPal
Предмет: Қазақ тiлi,
автор: karzaupovainkaraj
Предмет: Математика,
автор: Улька1103
Предмет: Химия,
автор: korovkayanka000