Предмет: Математика,
автор: Аноним
помогите пожалуйста)))))))))))))))))))))))))))))))))))))))))))
Приложения:



Ответы
Автор ответа:
0
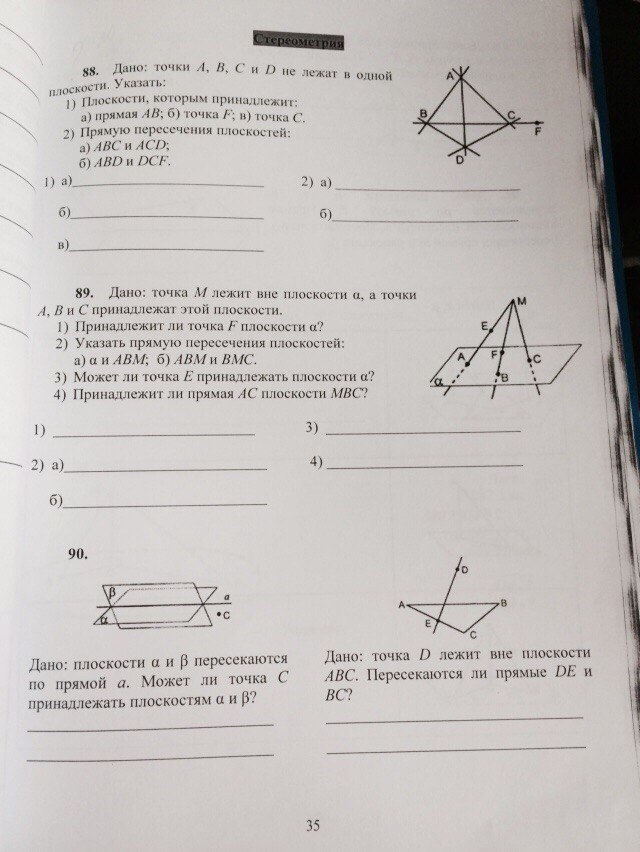
88.
1а) ABC, ABD
1б) BCD
1в) ABC, ACD, BCD
2а) АС
2б) BD
89.
1) F ∉ α
2а) AB
2б) BM
3) E ∉ α
4) AC ∉ MBC
90.
1) С не может принадлежать одновременно и α, и β
2) DE и BC не пересекаются
116.
1) 10! / 8! = 9·10 = 90
2) 11! / 5!·6! = 7·8·9·10·11 / 2·3·4·5 = 7·8·9·11 / 3·4 = 7·6·11 = 462
3) 6! / 4! = 5·6 = 30
4) 3! / 5! = 1 / 4·5 = 1/20 = 0,05
5) 10! / 5!·3! = 6·7·8·9·10 / 6 = 7·8·9·10 = 56·90 = 5040
6) 8! / 6! = 7·8 = 56
7) 4!+5! / 5!-4! = 4!·(1+5) / 4!·(5-1) = 6/4 = 3/2 = 1,5
8) 8!-7! / 7! = 7!·(8-1)/7! = 8 - 1 = 7
117.1.
n!/(n - 2)! = 2n
ОДЗ: n ≥ 2, n ∈ N
(n - 1)·n = 2n
n² - 3n = 0
n·(n - 3) = 0
n = 0, n = 3
С учётом области определения, n = 3.
117.2
(m + 2)! / m! = 72
ОДЗ: m ≥ 0
(m + 1)(m + 2) = 72
m² + 3m - 70 = 0
По т. Виета: m = -10, m = 7.
С учётом области определения, m = 7.
117.3
(k + 1)!/(k - 1)! = 30
ОДЗ: k ≥ 1, k ∈ N
k·(k + 1) = 30
k² + k - 30 = 0
По т. Виета: k = -6, k = 5.
С учётом области определения, k = 5.
117.4
(k - 2)!/(k - 4)! = 12
ОДЗ: k ≥ 4, k ∈ N
(k - 3)·(k - 2) = 12
k² - 5k - 6 = 0
По т. Виета: k = -1, k = 6.
С учётом области определения, k = 6.
118.1.
2, 4

118.2.
8, 3

118.3
1, 5

118.4
4, 6

115.1.
1500 об./мин.
115.2
Об./мин. 500 1000 1500 2000 2500 3000 3500
Н·м 20 55 100 140 140 140 140
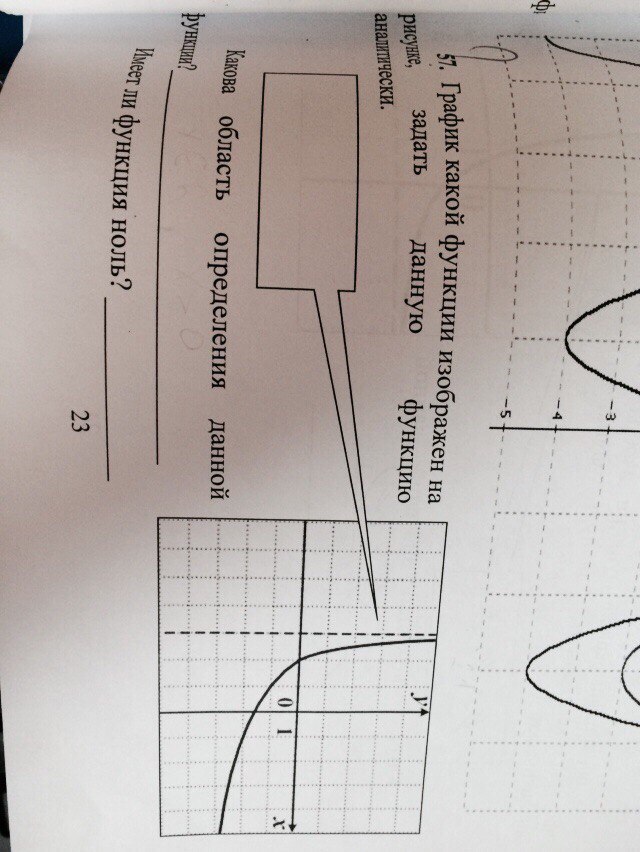
57.

x ∈ (-3; +∞)
y (-2) = 0
1а) ABC, ABD
1б) BCD
1в) ABC, ACD, BCD
2а) АС
2б) BD
89.
1) F ∉ α
2а) AB
2б) BM
3) E ∉ α
4) AC ∉ MBC
90.
1) С не может принадлежать одновременно и α, и β
2) DE и BC не пересекаются
116.
1) 10! / 8! = 9·10 = 90
2) 11! / 5!·6! = 7·8·9·10·11 / 2·3·4·5 = 7·8·9·11 / 3·4 = 7·6·11 = 462
3) 6! / 4! = 5·6 = 30
4) 3! / 5! = 1 / 4·5 = 1/20 = 0,05
5) 10! / 5!·3! = 6·7·8·9·10 / 6 = 7·8·9·10 = 56·90 = 5040
6) 8! / 6! = 7·8 = 56
7) 4!+5! / 5!-4! = 4!·(1+5) / 4!·(5-1) = 6/4 = 3/2 = 1,5
8) 8!-7! / 7! = 7!·(8-1)/7! = 8 - 1 = 7
117.1.
n!/(n - 2)! = 2n
ОДЗ: n ≥ 2, n ∈ N
(n - 1)·n = 2n
n² - 3n = 0
n·(n - 3) = 0
n = 0, n = 3
С учётом области определения, n = 3.
117.2
(m + 2)! / m! = 72
ОДЗ: m ≥ 0
(m + 1)(m + 2) = 72
m² + 3m - 70 = 0
По т. Виета: m = -10, m = 7.
С учётом области определения, m = 7.
117.3
(k + 1)!/(k - 1)! = 30
ОДЗ: k ≥ 1, k ∈ N
k·(k + 1) = 30
k² + k - 30 = 0
По т. Виета: k = -6, k = 5.
С учётом области определения, k = 5.
117.4
(k - 2)!/(k - 4)! = 12
ОДЗ: k ≥ 4, k ∈ N
(k - 3)·(k - 2) = 12
k² - 5k - 6 = 0
По т. Виета: k = -1, k = 6.
С учётом области определения, k = 6.
118.1.
2, 4
118.2.
8, 3
118.3
1, 5
118.4
4, 6
115.1.
1500 об./мин.
115.2
Об./мин. 500 1000 1500 2000 2500 3000 3500
Н·м 20 55 100 140 140 140 140
57.
x ∈ (-3; +∞)
y (-2) = 0
Похожие вопросы
Предмет: Геометрия,
автор: dinara0987
Предмет: Қазақ тiлi,
автор: kakashka645
Предмет: Физика,
автор: Ynazor451
Предмет: Алгебра,
автор: ad700900