Question

ДАЮ 80 БАЛЛОВ ЗА ЛЁГКОЕ ЗАДАНИЕ!!!!!!
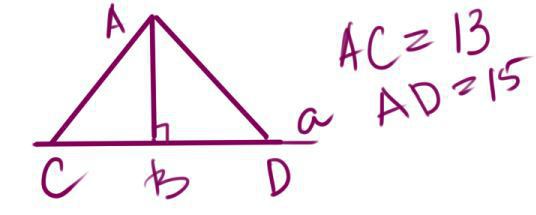
С точки к прямой проведено две наклонные, длины которых равны 13 см и 15 см.Найдите расстояние от точки до прямой, если разность проекций
наклонных на эту прямую равна 4 см.

Answer 1

Для треугольника ABC
AC^2=AB^2+BC^2 откуда AB^2-AC^2-BC^2
Пусть BC=x см. Тогда BD=x+4 см. 
Соответственно: AB^2=13^2-x^2
Аналогично для ABD
 AB^2=AD^2-BD^2
Соответственно: AB^2 = 15^2-(x+4)^2
А значит:
13^2-x^2=15^2-(x-4)^2
169-x^2=225-x^2-8x-16
-x^2+x^2+8x=225-16-169
8x=40
x=5.
Подставляем значения x
AB^2=13-5^2=169-25=144(12^2)
AB=12 см

Answer 2

спасибо солнышко