Question

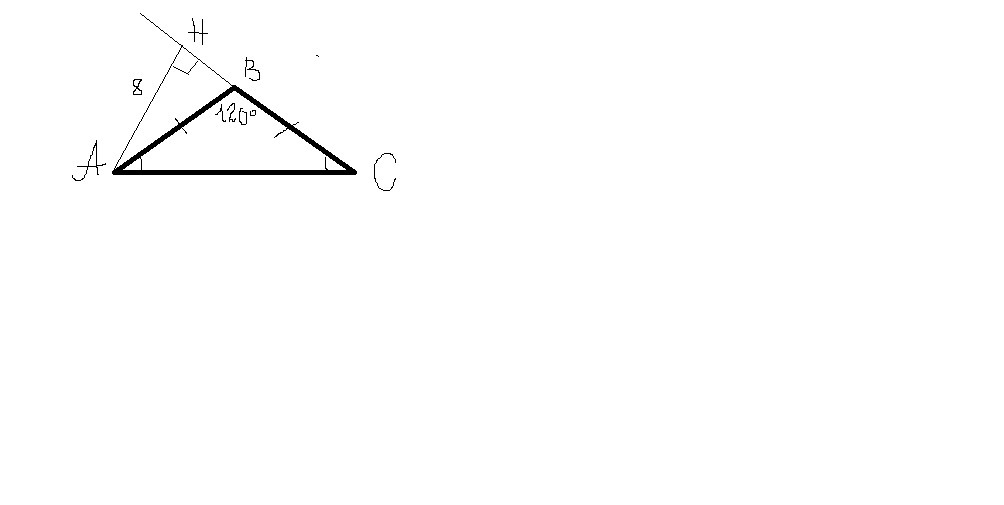
Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведенная к боковой стороне, равна 8 см. Найдите основание этого треугольника.

Answer 1

1) ΔАВС - равнобедренный, АВ=ВС , АС - основание , ∠В=120°, 
∠А=∠С = (180- 120)/2  = 30 °- углы при основании равны.

2) АН =8 см - высота к боковой стороне АВ ⇒∠Н=90°⇒
ΔАНС  -  прямоугольный , АС- гипотенуза ,  АН и НС - катеты.
Из пункта 1)   ∠С=30°.
Сторона , лежащая напротив угла в 30° равна половине гипотенузы:
АН = АС/2  ⇒ АС= 2 * АН
АС = 2*8= 16 см

Ответ:  АС= 16 см  - основание ΔАВС.

Чертёж ≈ , как в приложении.

Answer 2

Пусть дан рб треугольник АВС, с основанием АС.
СВ продлим вверх треугольника, тк высота АН =8 будет снаружи треугольника, тк АВС тупоугольный.
Рассмотрим Тр. АВН. Угол Н =90. внешний угол АВС=120 => угол НАВ=120-90=30.
Тогда НВ =половине АВ.
Пусть НВ=х, тогда АВ= 2х
Рассмотрим треугольники АВМ - ( ВМ - высота АВС к АС) и тр АВН.

АВ - общая,
Углы НАВ=ВАМ=30
Углы НВА=АВМ=60

=> треугольники равны => АМ =8 => АС=16.