Предмет: Геометрия,
автор: Garmonist
Помогите пожалуйста... Завтра писать тоже самое на контрольной!!!
1)Найдите угол между лучом ОВ и положительной полуосью ОХ, если В(3;3) 2)Решите треугольник ВСD, если угол В=45*: угол D=60* ; ВС=корень из 3 см. 3) Найдите косинусы углов А, В и С треугольника АВС, если А(3;9), В (0;6), С(4;2).
Приложения:
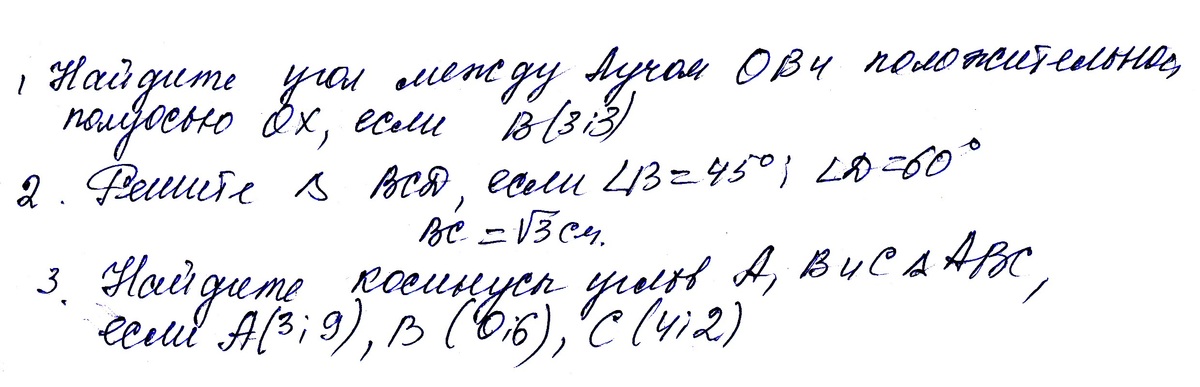
Ответы
Автор ответа:
0
Обе задачи простые. Главное - начерти рисунки правильно. (Из-за глюков - буду использовать русские буквы)
Первая задача. Тогда рассмотрим следующие треугольники: МКТ; НКТ; МНТ. Я рассмотрю подробно только один треугольник, так как с остальными разница чисто в буквах :) В треугольнике МКТ, ОП - средняя линия, так как она соединяет середины отрезков МТ и КТ. По теореме о средней линии ОП параллельно МК. Значит и в остальных треугольниках так же, то есть ОП параллельно МК, ОЕ параллельно НМ, ЕП параллельно НК. Отсюда следует, что плоскость ОПЕ параллельна плоскости КМН, так как попарно пересекающиеся прямые одной плоскости соответственно параллельны попарно пересекающимся прямым второй плоскости. Что и требовалось доказать! :)
Вторая задача: Задачу можно перенести на плоскость. Но это требует сильного теоретического обоснования, поэтому говорить буду Тебе без этой фигни - так тоже должно прокатить. Треугольники АОБ и ПОЦ подобны по двум углам - АОБ=ПОЦ, как вертикальные; ОБА=ЦПО, как перекрестные (кажется так называется) при параллельных ПЦ параллельно АБ (так как они из параллельных плоскостей и к тому же сами ещё в одной плоскости лежат). Значит найдём з подобия треугольников сторону ПЦ:
ПЦ:АБ = ПО:БО (как сторонам напротив равных углов) Значит ПЦ=ПО*АБ:БО=3*24:12=6 Ответ: 6. Готово! =)
Пост Скриптум: Вышли накладки с чертежом и условием. Условие не совсем точное - задачу можно решить только тогда, когда А и Ц принадлежат первой, а Б и Д - второй прямой. Рисуй и рассуждай только в этом случае.
Первая задача. Тогда рассмотрим следующие треугольники: МКТ; НКТ; МНТ. Я рассмотрю подробно только один треугольник, так как с остальными разница чисто в буквах :) В треугольнике МКТ, ОП - средняя линия, так как она соединяет середины отрезков МТ и КТ. По теореме о средней линии ОП параллельно МК. Значит и в остальных треугольниках так же, то есть ОП параллельно МК, ОЕ параллельно НМ, ЕП параллельно НК. Отсюда следует, что плоскость ОПЕ параллельна плоскости КМН, так как попарно пересекающиеся прямые одной плоскости соответственно параллельны попарно пересекающимся прямым второй плоскости. Что и требовалось доказать! :)
Вторая задача: Задачу можно перенести на плоскость. Но это требует сильного теоретического обоснования, поэтому говорить буду Тебе без этой фигни - так тоже должно прокатить. Треугольники АОБ и ПОЦ подобны по двум углам - АОБ=ПОЦ, как вертикальные; ОБА=ЦПО, как перекрестные (кажется так называется) при параллельных ПЦ параллельно АБ (так как они из параллельных плоскостей и к тому же сами ещё в одной плоскости лежат). Значит найдём з подобия треугольников сторону ПЦ:
ПЦ:АБ = ПО:БО (как сторонам напротив равных углов) Значит ПЦ=ПО*АБ:БО=3*24:12=6 Ответ: 6. Готово! =)
Пост Скриптум: Вышли накладки с чертежом и условием. Условие не совсем точное - задачу можно решить только тогда, когда А и Ц принадлежат первой, а Б и Д - второй прямой. Рисуй и рассуждай только в этом случае.
Похожие вопросы
Предмет: Русский язык,
автор: mstars07
Предмет: История,
автор: dentop899
Предмет: Алгебра,
автор: 3x2tibfasg
Предмет: Биология,
автор: Tamiris20