Запишите уравнение прямой и постройте её, если известно, что: а) Угловой коэффициент прямой равен -2 и она проходит через точку (2;-2).
Ответы
через точку (2;-2) проходит бесконечное множество прямых,
каждая имеет СВОЙ угол наклона к оси ОХ - это задается угловым коэффициентом
угловой коэффициент k= - 2
Уравнение прямой, проходящей через данную точку (x1, y1) в данном направлении, определяемом угловым коэффициентом k и координатами точки
y - y1 = k(x - x1).
подставим
y - (-2) = - 2(x - 2)
y+2 = -2x +4
y= -2x +2 или в другом виде y+2x-2=0
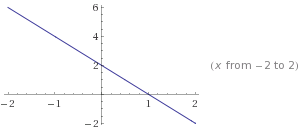
смотри рисунок во вложении
Уравнение прямой с угловым коефициентом имеет вид
Согласно условию k=-2
Подставим координаты точки и нйдем
Уравнение прямой имеет вид
Построить прямую можна по двум точкам, одна есть в условии (2; -2). Для второй подставим x=0
Вторая точка (0; 2)
