Предмет: Алгебра,
автор: Saadeerica
Ребят, просьба помочь решить 10 тригонометрических уравнений.Ошибаться нельзя-решается судьба годовой оценки.
Приложения:
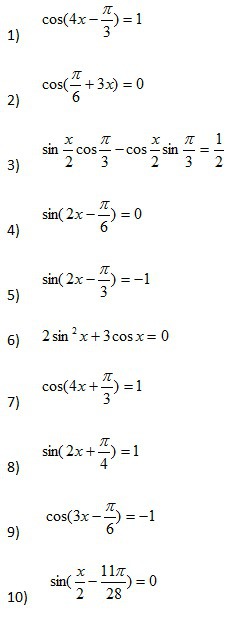
Ответы
Автор ответа:
0
1)Cos(4x - π/3) = 1
4x - π/3 = 2πk, k ∈Z
4x = 2πk + π/3, k ∈Z
x = πk/2 + π/12, k∈Z
2)Cos(π/6 +3х) = 0
π/6 +3х = π/2 + πk , к ∈Z
3x = π/2 + πk - π/6, k ∈Z
3x = π/3 + πk, k ∈Z
x = π/9 + πk/3, k ∈Z
3)Sin(x/2 - π/3) = 1/2
х/2 - π/3 = (-1)^n arcSin1/2 + nπ, n ∈Z'
x/2 -π/3 = (-1)^n π/6 + πn, n ∈Z
x/2 = (-1)^n π/6 + πn + π/3, n ∈Z
x = (-1)^n π/3 + 2πn + 2π/3 , n ∈Z
4)Sin(2x - π/6) = 0
2х - π/6 = nπ, n ∈Z
2x = nπ + π/6, n∈Z
x = nπ/2 + π/12, n ∈Z
5)Sin(2x -π/3) = -1
2х - π/3 = -π/2 + 2πk ,к ∈Z
2x = π/3 -π/2 + 2πk, k ∈Z
x = π/6 -π/4 + πk, k ∈Z
6) 2Sin² x +3Cosx = 0
2(1-Cos²x) + 3Cosx = 0
2 - 2Cos²x + 3Cosx = 0
2Cos²x -3Cosx - 2 = 0 Решаем как квадратное
а)Соs x = 2 (нет решений)
б) Сos x = -1/2
х = +-arcCos(-1/2) + 2πk, k ∈Z
x = +- 2π/3 + 2πk, k ∈Z
7)Cos(4x + π/3) = 1
4x + π/3 = 2πk, k ∈Z
4x = 2πk - π/3, k ∈Z
x = πk/2 - π/12, k∈Z
8) Sin(2x + π/4) = 1
2х + π/4 = π/2 + 2πк, к ∈Z
2x = -π/4 +π/2 + 2πк, к ∈Z
x = -π/8 + π/4+ πк, к ∈Z
9) Cos(3x - π/6) = -1
3x - π/6 = π + 2πк , к ∈Z
3x = π/6 + π + 2πк , к ∈Z
3x =7π/6 + 2πк , к ∈Z
x = 7π/18 +2πк/3, к ∈Z
10) Sin(x/2 + 11π/28) = 0
х/2 + 11π/28 = nπ, n ∈Z
x/2 = nπ - 11π/28, n∈Z
x =2 nπ - 11π/14, n ∈Z
4x - π/3 = 2πk, k ∈Z
4x = 2πk + π/3, k ∈Z
x = πk/2 + π/12, k∈Z
2)Cos(π/6 +3х) = 0
π/6 +3х = π/2 + πk , к ∈Z
3x = π/2 + πk - π/6, k ∈Z
3x = π/3 + πk, k ∈Z
x = π/9 + πk/3, k ∈Z
3)Sin(x/2 - π/3) = 1/2
х/2 - π/3 = (-1)^n arcSin1/2 + nπ, n ∈Z'
x/2 -π/3 = (-1)^n π/6 + πn, n ∈Z
x/2 = (-1)^n π/6 + πn + π/3, n ∈Z
x = (-1)^n π/3 + 2πn + 2π/3 , n ∈Z
4)Sin(2x - π/6) = 0
2х - π/6 = nπ, n ∈Z
2x = nπ + π/6, n∈Z
x = nπ/2 + π/12, n ∈Z
5)Sin(2x -π/3) = -1
2х - π/3 = -π/2 + 2πk ,к ∈Z
2x = π/3 -π/2 + 2πk, k ∈Z
x = π/6 -π/4 + πk, k ∈Z
6) 2Sin² x +3Cosx = 0
2(1-Cos²x) + 3Cosx = 0
2 - 2Cos²x + 3Cosx = 0
2Cos²x -3Cosx - 2 = 0 Решаем как квадратное
а)Соs x = 2 (нет решений)
б) Сos x = -1/2
х = +-arcCos(-1/2) + 2πk, k ∈Z
x = +- 2π/3 + 2πk, k ∈Z
7)Cos(4x + π/3) = 1
4x + π/3 = 2πk, k ∈Z
4x = 2πk - π/3, k ∈Z
x = πk/2 - π/12, k∈Z
8) Sin(2x + π/4) = 1
2х + π/4 = π/2 + 2πк, к ∈Z
2x = -π/4 +π/2 + 2πк, к ∈Z
x = -π/8 + π/4+ πк, к ∈Z
9) Cos(3x - π/6) = -1
3x - π/6 = π + 2πк , к ∈Z
3x = π/6 + π + 2πк , к ∈Z
3x =7π/6 + 2πк , к ∈Z
x = 7π/18 +2πк/3, к ∈Z
10) Sin(x/2 + 11π/28) = 0
х/2 + 11π/28 = nπ, n ∈Z
x/2 = nπ - 11π/28, n∈Z
x =2 nπ - 11π/14, n ∈Z
Автор ответа:
0
Извините, но в 10 (sin x/2-11п/28), но всё равно спасибо вам большое!
Похожие вопросы
Предмет: Математика,
автор: umarbaevasaodat
Предмет: Геометрия,
автор: 2011naz
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Кисарыбка
Предмет: Обществознание,
автор: ana7008