Предмет: Геометрия,
автор: KortiTyan
Помогите решить задачу по геометрии пожалуйста, желательно с дано и чертежом!
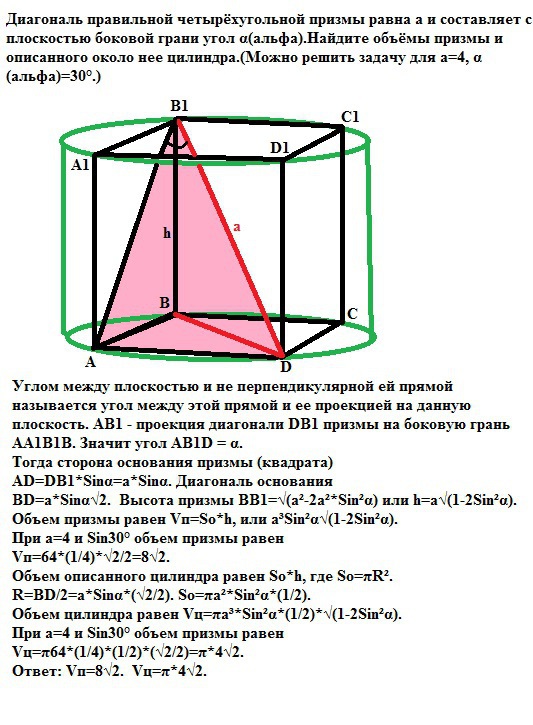
Диагональ правильной четырёхугольной призмы равна а и составляет с плоскостью боковой грани угол α(альфа).Найдите объёмы призмы и описанного около нее цилиндра.(Можно решить задачу для а=4, α(альфа)=300.)
Ответы
Автор ответа:
0
Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость. АВ1 - проекция диагонали DB1 призмы на боковую грань АА1В1В. Значит угол АВ1D = α.
Тогда сторона основания призмы (квадрата)
АD=DB1*Sinα=а*Sinα. Диагональ основания
ВD=а*Sinα√2. Высота призмы ВВ1=√(а²-2а²*Sin²α) или h=а√(1-2Sin²α).
Объем призмы равен Vп=So*h, или а³Sin²α√(1-2Sin²α).
При а=4 и Sin30° объем призмы равен
Vп=64*(1/4)*√2/2=8√2.
Объем описанного цилиндра равен So*h, где So=πR².
R=BD/2=а*Sinα*(√2/2). So=πа²*Sin²α*(1/2).
Объем цилиндра равен Vц=πа³*Sin²α*(1/2)*√(1-2Sin²α).
При а=4 и Sin30° объем призмы равен
Vц=π64*(1/4)*(1/2)*(√2/2)=π*4√2.
Ответ: Vп=8√2. Vц=π*4√2.
Тогда сторона основания призмы (квадрата)
АD=DB1*Sinα=а*Sinα. Диагональ основания
ВD=а*Sinα√2. Высота призмы ВВ1=√(а²-2а²*Sin²α) или h=а√(1-2Sin²α).
Объем призмы равен Vп=So*h, или а³Sin²α√(1-2Sin²α).
При а=4 и Sin30° объем призмы равен
Vп=64*(1/4)*√2/2=8√2.
Объем описанного цилиндра равен So*h, где So=πR².
R=BD/2=а*Sinα*(√2/2). So=πа²*Sin²α*(1/2).
Объем цилиндра равен Vц=πа³*Sin²α*(1/2)*√(1-2Sin²α).
При а=4 и Sin30° объем призмы равен
Vц=π64*(1/4)*(1/2)*(√2/2)=π*4√2.
Ответ: Vп=8√2. Vц=π*4√2.
Приложения:
Похожие вопросы
Предмет: Немецкий язык,
автор: pavuukparker
Предмет: Биология,
автор: tatenovaruslana
Предмет: Музыка,
автор: zhaniya82
Предмет: География,
автор: kristinacom47
Предмет: История,
автор: анжеличка123