Предмет: Геометрия,
автор: ВладEagle
Сложная задача!
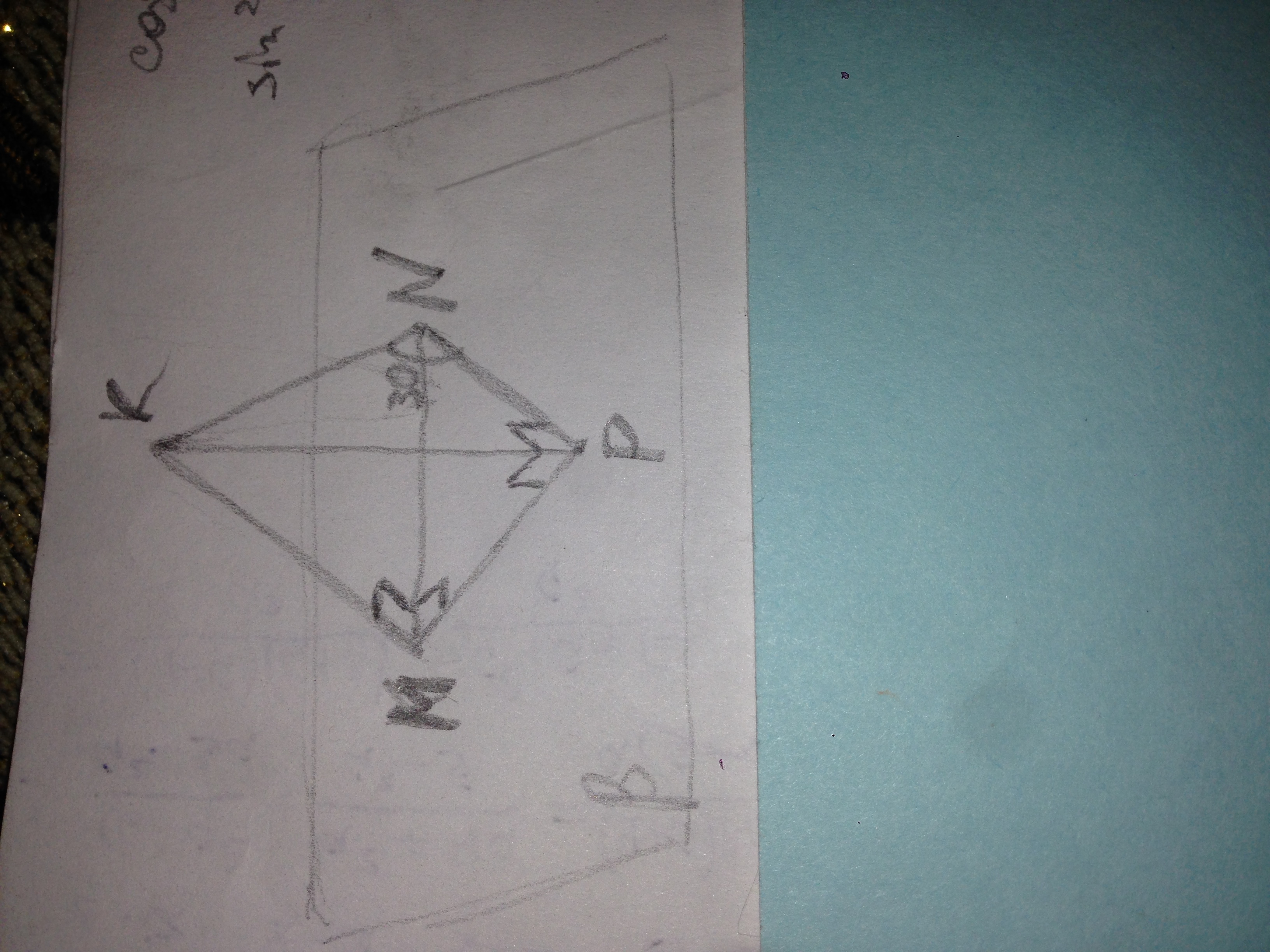
Плоскость β проходит через сторону MN треугольника MKN. Сторона KN образует с плоскостью β угол 30°. Найти синус угла между плоскостями β и MKN, если MK= 12, KN= 13, MN= 5.
Ответы
Автор ответа:
0
Треугольник МКН прямоугольный (13²=12²+5²), ∠КМН=90°.
Опустим перпендикуляр КР на плоскость β. ∠КНР=30°
В тр-ке КНР КР=КН·sin30=13/2=6.5
В тр-ке КРМ sinM=КР/КМ=6.5/12=13/24 - это ответ.
Опустим перпендикуляр КР на плоскость β. ∠КНР=30°
В тр-ке КНР КР=КН·sin30=13/2=6.5
В тр-ке КРМ sinM=КР/КМ=6.5/12=13/24 - это ответ.
Приложения:
Автор ответа:
0
Правильный
Автор ответа:
0
А КМ не перпендикуляр на плоскость β?
Автор ответа:
0
нет, поэтому мы и вычисляем угол КМР
Похожие вопросы
Предмет: Русский язык,
автор: rizaa26
Предмет: Математика,
автор: masyanuweregood
Предмет: Қазақ тiлi,
автор: gulzhanar2008ggggj3
Предмет: Литература,
автор: antontomin013
Предмет: Биология,
автор: nastyanvkz456