Question

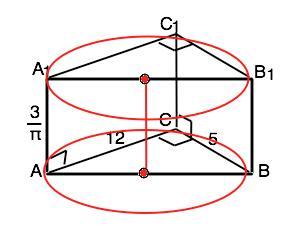
В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 12. Боковые ребра призмы равны 3/П . Найдите площадь боковой поверхности описанного цилиндра

Answer 1

Ответ: 39 (ед. площади)

Объяснение: Боковые ребра прямой призмы перпендикулярны основанию. Высота прямой призмы равна длине бокового ребра.

  Отношение катетов ∆ АВС – АС:ВС=12:5, что указывает на то, что его стороны из Пифагоровых троек с отношением сторон 12:5:13. Гипотенуза АВ=13 (можно проверить по т.Пифагора).

. Гипотенуза АВ=13, она же - диаметр основания. => R=6,5, а высота цилиндра равна высоте призмы, т.е. длин Центром основания цилиндра, описанного около призмы, в основании которой прямоугольный треугольник, является середина гипотенузы. Гипотенуза AB=2R=d=13, высота цилиндра равна высоте призмы, т.е. длине её бокового ребра. Ѕ(бок. цил.)=π•d•h

Ѕ(бок)=π•13•3/π=39 (ед. площади).