Предмет: Геометрия,
автор: aartemm
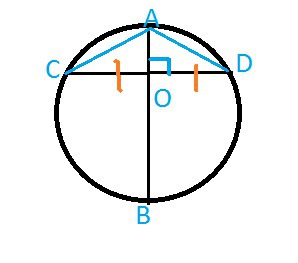
В окружности проведены диаметр АВ и хорда СD, перпендикулярная диаметру. Докажите, что треугольники ADC и DBC равнобедренные.
Ответы
Автор ответа:
0
По первому свойству хорд (Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам) CO=OD.
Рассмотрим ΔAOC и ΔAOD:
CO=OD, AO - общая сторона. ∠AOC=∠AOD= 90° ⇒(по двум сторонам и углу между ними) ΔAOC=ΔAOD⇒ AC=AD ⇒ ΔADC- равнобедренный.
Аналогично с ΔDBC
Рассмотрим ΔAOC и ΔAOD:
CO=OD, AO - общая сторона. ∠AOC=∠AOD= 90° ⇒(по двум сторонам и углу между ними) ΔAOC=ΔAOD⇒ AC=AD ⇒ ΔADC- равнобедренный.
Аналогично с ΔDBC
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: oksana23885
Предмет: Математика,
автор: aknurasylbek4
Предмет: Математика,
автор: MakhmudovaAmina