Кто может решить 5 логарифмических уравнений??
ФОТОГРАФИЯ ПРИМЕРОВ!
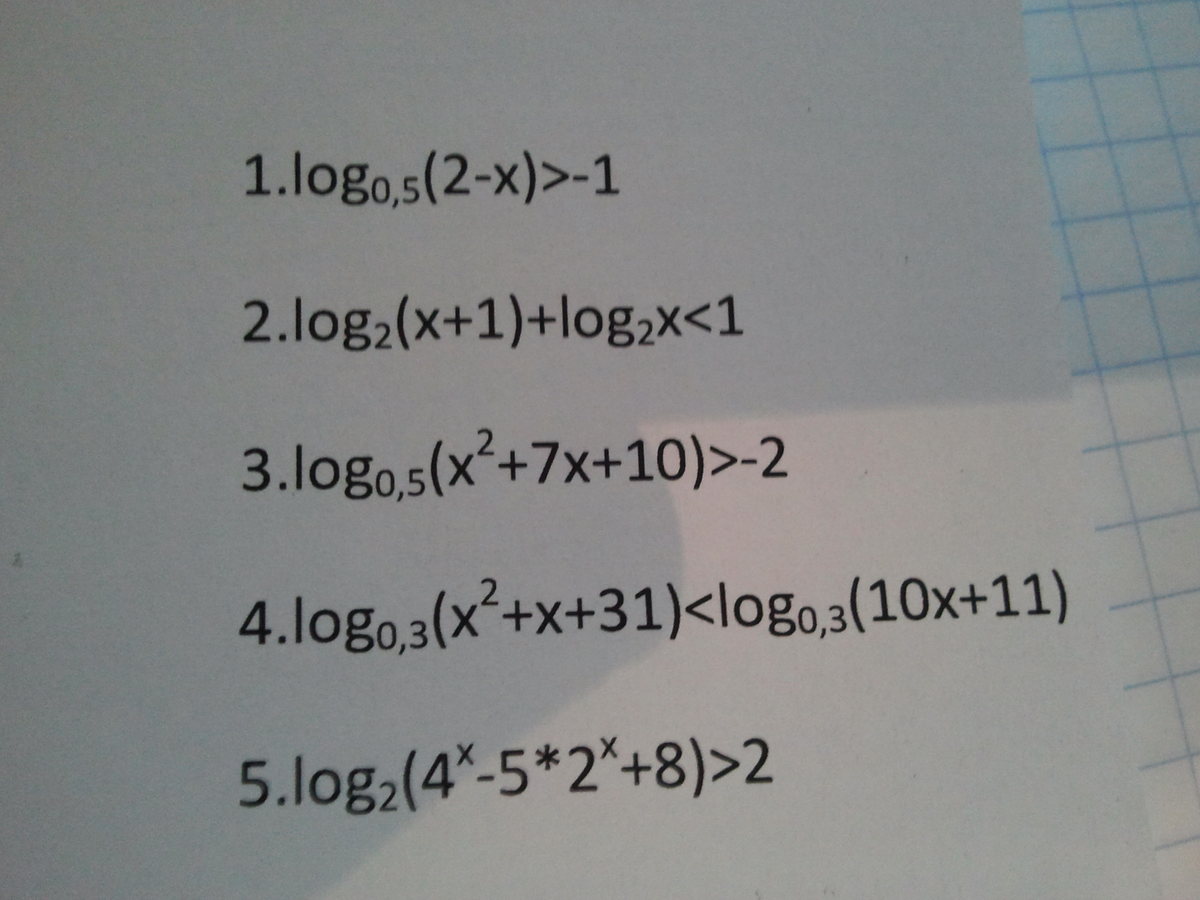
Ответы
dj dkjltybz[//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////


Начнем с того, что это не уравнения, а неравенства.
1)ОДЗ: 2-х>0,х<2
2-x<2, 0<x, x>0 ⇒x∈(0,2)
2) ОДЗ: х+1>0 и х>0 ⇒х>0
х(х+1)<2, х²+х-2<0, х₁=1, х₂=-2
(х-1)(х+2)<0 ⇒ х∈(-2,1)
Учтя ОДЗ получим окончательно х∈(0,1)
3)ОДЗ: х²+7х+10>0 (х+2)(х+5)>0 ⇒ х∈(-∞,-5)∨(-2,+∞)
х>+7х+10<4, х²+7х+6<0, (х+6)(х+1)<0 ⇒ х∈(-6,-1)
Учтя ОДЗ: х∈(-6,-5)
4) ОДЗ: 4^x-5*2^x+8>0 Здесь D=25-32=-7<0 ⇒ это выражение >0 при х∈(-∞,+∞)
(2^x)^2-5*2^x+8>4, t=2^x, t²-5t+4>0 (t-1)(t-4)>0 ⇒ t∈(-∞,1)∨(4,+∞)
2^x<1,2^x<2⁰, x<0 или 2^x>4, 2^x>2², x>2
Ответ: х∈(-∞0)∨(2,+∞)

