Предмет: Алгебра,
автор: katyamatveeva
даю 99 балов
Один пример на фото,тема:решение тригонометрических уравнений
решите подробно,пожалуйста
Приложения:
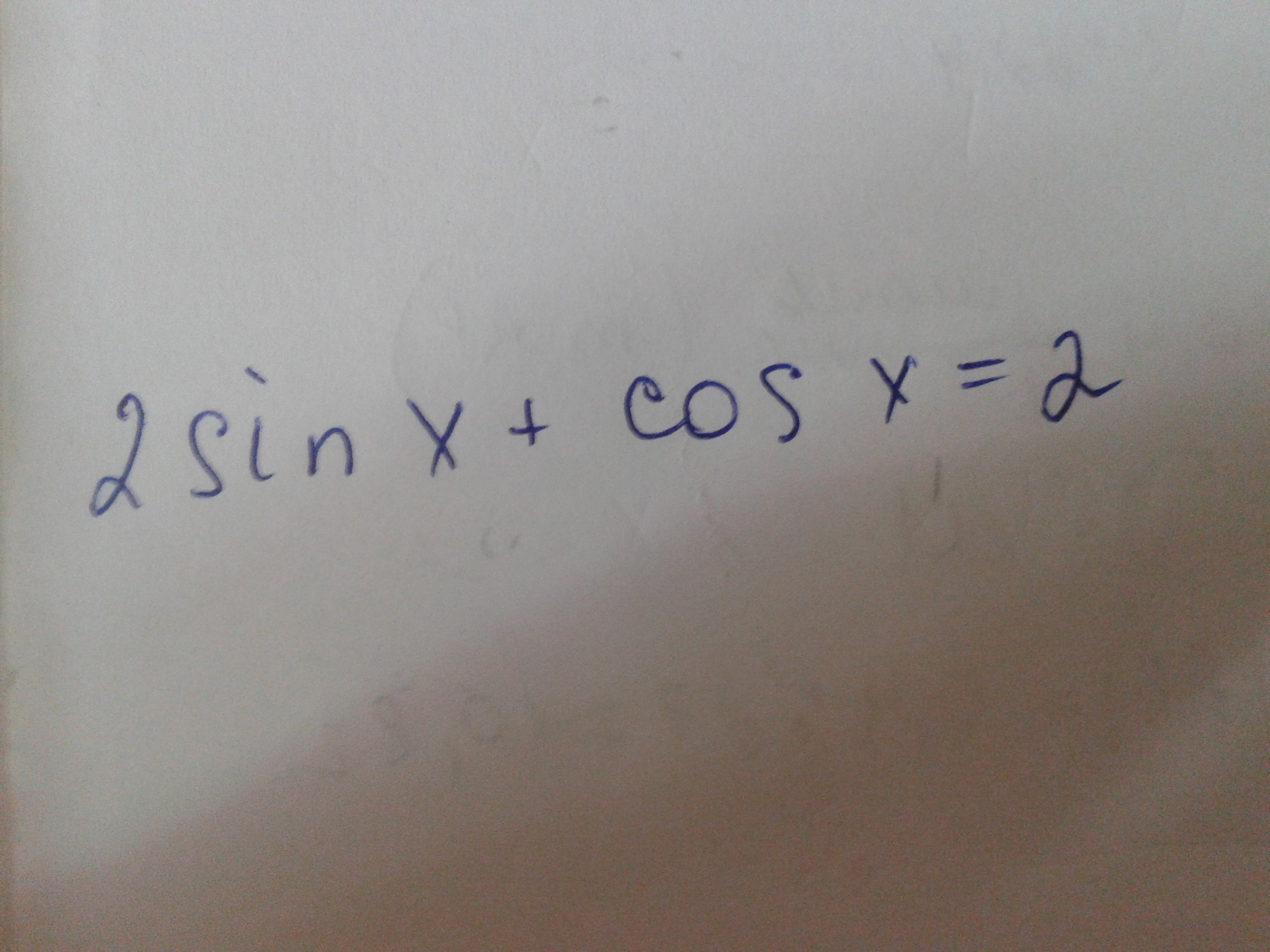
Ответы
Автор ответа:
0
2*2sin(x/2)cos(x/2)+cos²(x/2)-sin²(x/2)-2*(sin²(x/2)+cos²(x/2))=0
4sin(x/2)cos(x/2)+cos²(x/2)-sin²(x/2)-2sin²(x/2)-2cos²(x/2)=0
3sin²(x/2)-4sin(x/2)cos(x/2)+cos²(x/2)=0 /cos²(x/2)
3tg²(x/2)-4tg(x/2)+1=0
tg(x/2)=a
3a²-4a+1=0
D=16-12=4
a1=(4-2)/6=1/3⇒tg(x/2)=1/3⇒x/2=arctg1/3+πn⇒x=2arctg1/3+2πn,n∈z
a2=(4+2)/6=1⇒tg(x/2)=1⇒x/2=π/4+πk⇒x=π/2+2πk,k∈z
4sin(x/2)cos(x/2)+cos²(x/2)-sin²(x/2)-2sin²(x/2)-2cos²(x/2)=0
3sin²(x/2)-4sin(x/2)cos(x/2)+cos²(x/2)=0 /cos²(x/2)
3tg²(x/2)-4tg(x/2)+1=0
tg(x/2)=a
3a²-4a+1=0
D=16-12=4
a1=(4-2)/6=1/3⇒tg(x/2)=1/3⇒x/2=arctg1/3+πn⇒x=2arctg1/3+2πn,n∈z
a2=(4+2)/6=1⇒tg(x/2)=1⇒x/2=π/4+πk⇒x=π/2+2πk,k∈z
Автор ответа:
0
ОГРОМНЕЙШЕЕ СПАСИБОООО!!!!!!!!!!!!!
Похожие вопросы
Предмет: Математика,
автор: albagachiev75
Предмет: Английский язык,
автор: evafilatova08
Предмет: Английский язык,
автор: eliseimik
Предмет: География,
автор: егор5355