Предмет: Алгебра,
автор: arrrrrina
прошууууу
помогииите
у меня сейчас мозг взорвется
температура 38.7, а мама уроки делать заставляет;(
верхние два нужно представить в виде произведения, а нижний один нужно доказать что при любых значениях "х" выражение принимает положительное значение
Приложения:
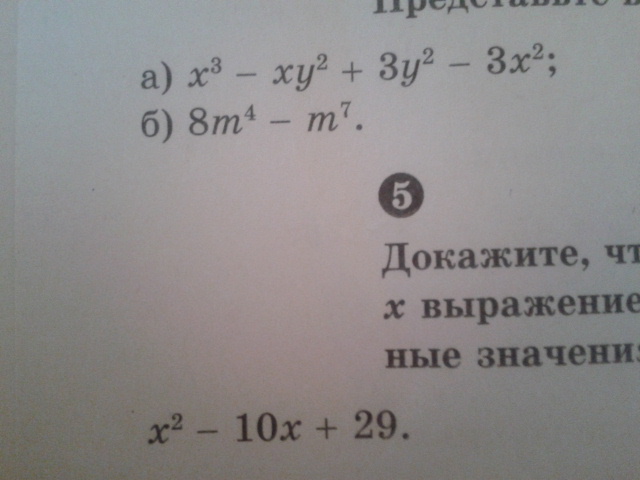
Ответы
Автор ответа:
0
1. x^3-xy^2+3y^2-3x^2
группируем x^3 с -3x^2,а -xy^2 с 3y^2. Получим y^2(3-х) и x^2(x-3). Чтобы группировать, в скобках должны быть одинаковые числа. Поэтому y^2(3-х) мы умножаем на -1 и получаем -y^2(х-3). И группируем окончательно: (x^2-y^2)(х-3)
2. 8m^4-m^7=m^4(8-m^3)
Автор ответа:
0
а) ... = x(x^2-y^2) - 3(x^2-y^2) = (x^2-y^2)(x-3) = (x-y)(x+y)(x-3) формула разность квадратов
b) ... = m^4(8-m^3) = m^4(2-m)(4+2m+m^2) формула разность кубов
x^2 - 10x +29
D = 100 - 4*29 = 100 - 116 < 0 => корней уравнение не имеет => график функции (парабола) ось ОХ не пересекает, ветви параболы направлены вверх (т.к. коэффициент при x^2 = 1 > 0) => парабола расположена выше оси ОХ, т.е. значения функции никогда не бывают отрицательными
Похожие вопросы
Предмет: Химия,
автор: xony456
Предмет: История,
автор: comc44131
Предмет: Русский язык,
автор: gizikovam
Предмет: Физика,
автор: Mihan97