Предмет: Алгебра,
автор: Незнайка7681
Исследовать функцию и построить ее график
Ответы
Автор ответа:
0
1.
функция нечетная
2.
наклонных асимптот нет
идем влево - график уходит далеко вверх
идем вправо - график уходит далеко вниз
любое число
3.
Точки пересечения с осью ОХ
4.
__-__
5.
__+__0__-__
7.
Дополнительные точки
x | 2 | -2 |
y |-6 | 6 |
График прилагается
Приложения:
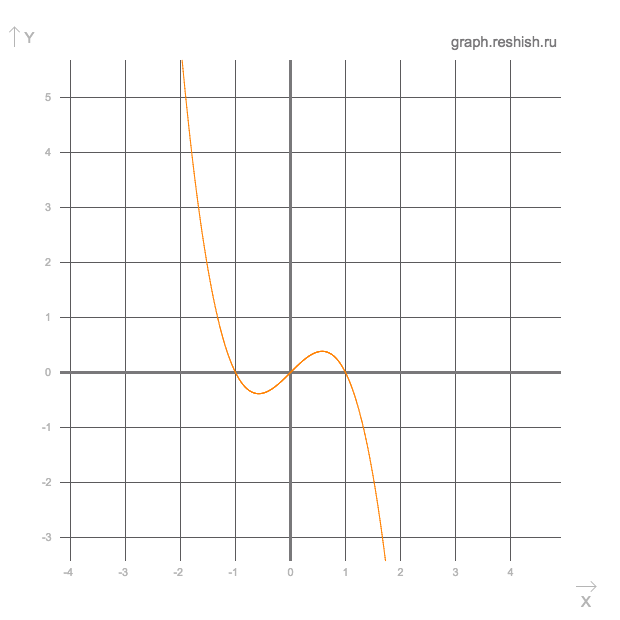
Автор ответа:
0
Это по действиям да получается?)
Автор ответа:
0
чтобы было понятно, что за чем идёт
Автор ответа:
0
спасибо)))
Автор ответа:
0
обращайтесь) всегда пожалуйста
Похожие вопросы
Предмет: Алгебра,
автор: SMsKa10
Предмет: Українська мова,
автор: urijhmilevskij5
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: ДашикКарандашик
Предмет: Алгебра,
автор: dasha278258