Question

Решите пожалуйста номер 4.6.5. Заранее спасибо.

Answer 1

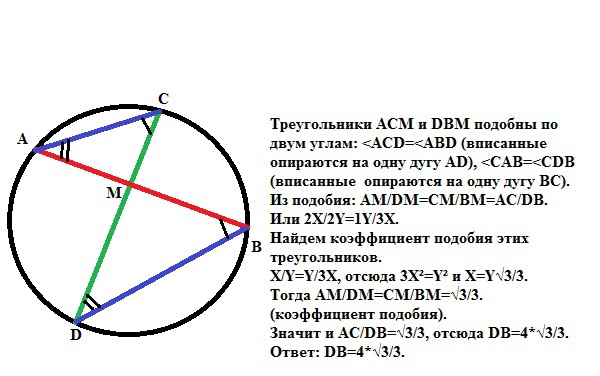
Треугольники АСМ и DBM подобны по двум углам: <ACD=<ABD (вписанные  опираются на одну дугу АD), <CAB=<CDB  (вписанные  опираются на одну дугу BC).
Из подобия: AM/DM=CM/BM=AC/DB.
Или 2X/2Y=1Y/3X.
Найдем коэффициент подобия этих треугольников.
Х/Y=Y/3X, отсюда 3X²=Y² и Х=Y√3/3.
Тогда AM/DM=CM/BM=√3/3. (коэффициент подобия).
Значит и АС/DB=√3/3, отсюда DB=4*√3/3.
Ответ: DB=4*√3/3.