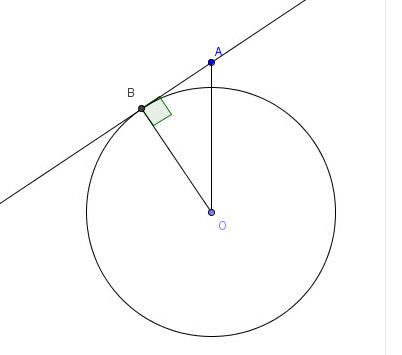
1 ) Из точки А к окружности с центром в точке О проведена касательная АВ (В-точка касания ) . Найдите АО , если радиус окружности ранен 12 корень 2 см , а <OAB=45 градусов
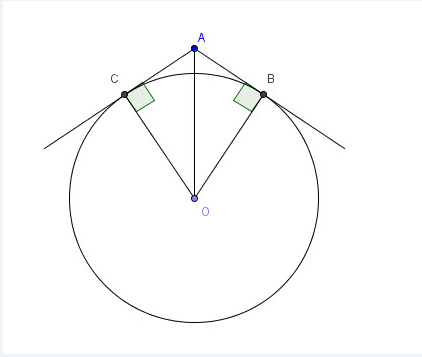
2) К окружности с центррм в точке О и радиусом 5 см из тоочки А проведены две касательные АВ и АС (В и С -точки касания) .Найдите <BAC , если АВ= 5 корень 3 см
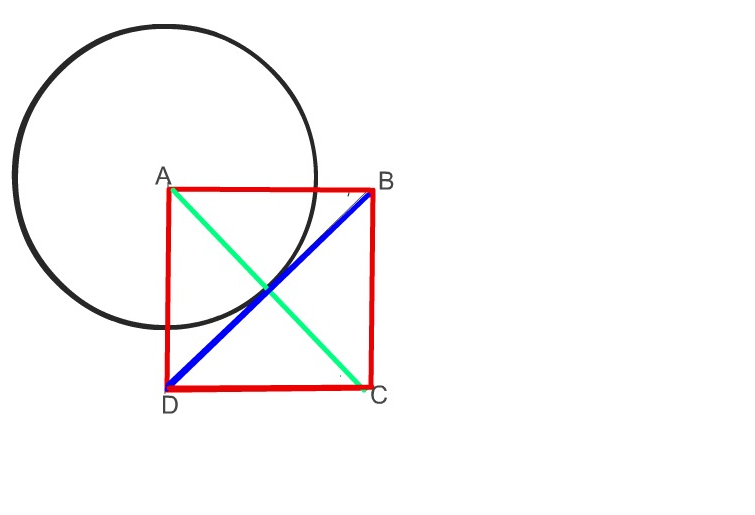
3) Вершина А квадрата АВСД является центром окружности , радиус которой равен половине диоганали квадрата . Докажите , что прмая ВД
является касательной к этой окружности .
Ответы
Треугольник АОВ прямоугольный, равнобедренный, угол А=45 = углуО = 90-45=45
ОВ=АВ= 12 х корень2, АО - гипотенуза = корень (АВ в квадрате +ОВ в квадрате)=
=корень (288+288) =24
Треугольник АВО прфмоугольный, ОВ=5, АВ = 5 х корень3, АО - гипотенуза =
=корень (ОВ в квадрате + АВ в квадрате) = корень (25+75)=10
катетОВ в два раза меньше гипотенузы и лежит напротив угла 30 град.
угол ОАВ=30
Диагонали в квадрате перпендикулярны друг другу. Прямая, которая перпендикулярна к диаметру окружности ы проходит через его конец - это касательная к этой окружности