Предмет: Алгебра,
автор: gag99
Помогите пожалуйста!!!!!!!!!!!!!!
Приложения:
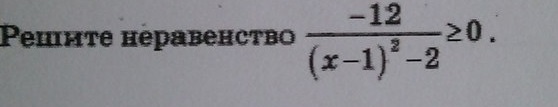
Ответы
Автор ответа:
0
12/(x-1)²-2≤0
12/(x-1-√2)(x-1+√2)
отмечай на координатной прямой точки 1-√2 и 1+√2
Расставляй знаки, начиная с права + - +
Ответ [1-√2;1+√2]
12/(x-1-√2)(x-1+√2)
отмечай на координатной прямой точки 1-√2 и 1+√2
Расставляй знаки, начиная с права + - +
Ответ [1-√2;1+√2]
Автор ответа:
0
Ваш ответ неверный. "Квадратные" скобки означают, что концы интервала тоже удовлетворяют неравенству, но это не так, поскольку здесь знаменатель дроби обращается в 0. скобки должны быть "круглыми", которые показывают, что концы интервала не учитываются.
Автор ответа:
0
Так как знаменатель дроби не может равняться нулю, а в числителе стоит не равное нулю число, то -12/((x-1)²-2)) ≠0. Поэтому будем решать неравенство -12/((x-1)²-2)>0. Очевидно, что для этого должно выполняться неравенство (x-1)²-2<0. Это неравенство приводится к виду x²-2x+1-2=x²-2x-1<0. Решим уравнение x²-2x-1=0. Дискриминант D=(-2)²-4*1*(-1)=8=(2*√2)², откуда x1=(2+2*√2)/2=1+√2, x2=(2-2*√2)/2=1-√2. В точках x1 и x2 знаменатель дроби обращается в 0, поэтому эти точки не удовлетворяют неравенству. При x<1-√2 (x-1)²-2>0, при 1-√2<x<1+√2 (x-1)²-2<0, при x>1+√2 (x-1)²-2>0. Значит, неравенство выполняется лишь при 1-√2<x<1+√2, т.е. на интервале (1-√2;1+√2)
Ответ: x∈(1-√2;1+√2).
Ответ: x∈(1-√2;1+√2).
Похожие вопросы
Предмет: Английский язык,
автор: alfahaker09
Предмет: Другие предметы,
автор: zevrwenz
Предмет: География,
автор: AlikPlay2006
Предмет: Алгебра,
автор: tomik666
Предмет: Литература,
автор: mikhaylenko00