Предмет: Алгебра,
автор: DeN1770
Помогите с интегралом
решить по частям
Приложения:
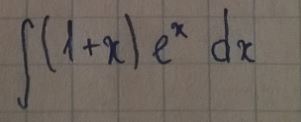
Ответы
Автор ответа:
0
Это несложный интеграл

Применим формулу интегрирования по частям:

Положим за , а за
, а за 
Тогда получим:

Подставляем в формулу и решаем:

Для проверки возьмем производную:

Применим формулу интегрирования по частям:
Положим за
Тогда получим:
Подставляем в формулу и решаем:
Для проверки возьмем производную:
Похожие вопросы
Предмет: География,
автор: zhantik562
Предмет: Английский язык,
автор: GOFMANVIOLETTA2
Предмет: Русский язык,
автор: abuzarovrabiym
Предмет: Математика,
автор: 201226