Предмет: Математика,
автор: Alinocha1308
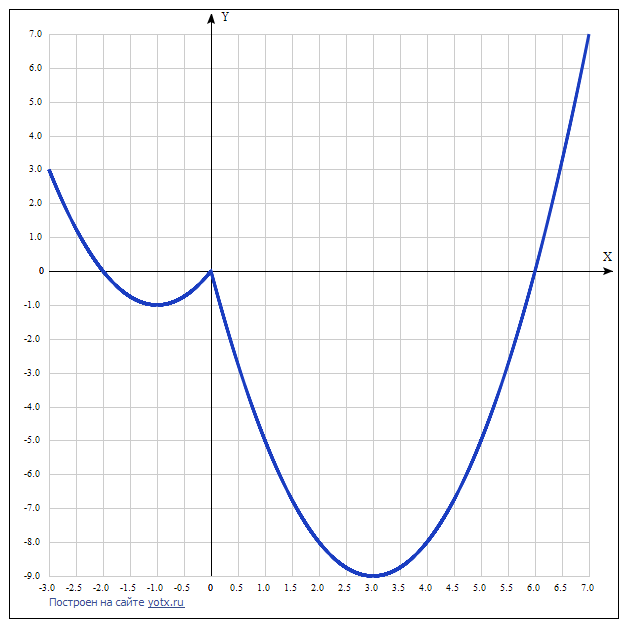
Постройте график функции y=x^2-4| x |-2x и определите, при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих
Ответы
Автор ответа:
0
Если у заданной функции y=x²-4| x |-2x раскрыть модуль, то получим 2 функции:
y=x² - 4x - 2x = x² - 6x,
y=x² - 4(-x) - 2x = х² + 2х.
Так как у обеих функций коэффициент с=0, то их общей границей является начало координат.
График заданной функции представляет собой сочетание двух парабол. У левой параболы вершина находится в точке:
Хо = -в/2а = -(-6)/(2*1) = 3, Уо = 9-6*3 = -9.
У правой Хо = -2/2 = -1, Уо = 1 +2*(-1) = -1.
Ответ: прямая y=m имеет с графиком не менее одной, но не более трёх общих при -9 ≤ m ≤ -1.
y=x² - 4x - 2x = x² - 6x,
y=x² - 4(-x) - 2x = х² + 2х.
Так как у обеих функций коэффициент с=0, то их общей границей является начало координат.
График заданной функции представляет собой сочетание двух парабол. У левой параболы вершина находится в точке:
Хо = -в/2а = -(-6)/(2*1) = 3, Уо = 9-6*3 = -9.
У правой Хо = -2/2 = -1, Уо = 1 +2*(-1) = -1.
Ответ: прямая y=m имеет с графиком не менее одной, но не более трёх общих при -9 ≤ m ≤ -1.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: СтИк163
Предмет: Окружающий мир,
автор: daniilmira2010
Предмет: Математика,
автор: andrejtretakov16028
Предмет: Математика,
автор: 123655
Предмет: Математика,
автор: khafizova1969