Предмет: Алгебра,
автор: TopNeKek
Решите пожалуйста, тему давно прошел, уже не помню, как делать. Спасибо большое, если выполните.
Приложения:

Ответы
Автор ответа:
0
Использованы тригонометрические формулы, правила действий с алгебраическими дробями
Приложения:

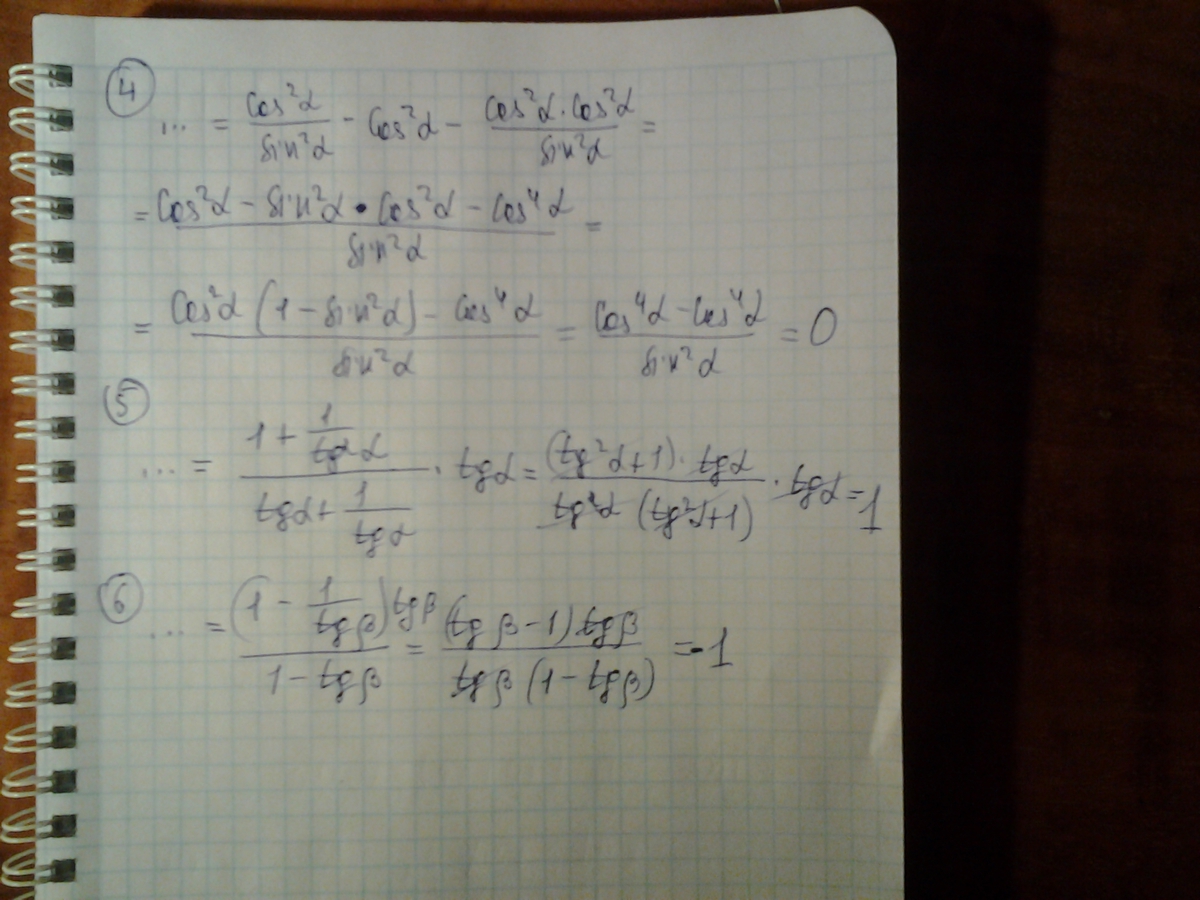
Автор ответа:
0
Спасибо
Автор ответа:
0
1) (tgα+ctgα)²-(tgα-ctgα)²=tg²α+2tgα·ctgα+ctg²α-tg²α+2tgα·ctgα-ctg²α=
=4tgα·ctgα=4;
2)tgα/(1+tg²α) -ctgα/(1+ctg²α)=tgα/(1/cos²α)-ctgα/(1/sin²α)=
=tgα·cos²α-ctgα·sin²α=(sinα/cosα)·cos²α-(cosα/sinα)·sin²α=
=sinαcosα-sinαcosα=0;
3)1/(1+tg²α)+1/(1+ctg²α)=1/(1/cos²α)+1/(1/sin²α)=
=cos²α+sin²α=1;
4)ctg²α-cos²α-ctg²α·cos²α=ctg²α-cos²α(1+ctg²α)=
=ctg²α-cos²α·(1/sin²α)=ctg²α-ctg²α=0;
5)[(1+ctg²α)/(tgα+ctgα)]·tgα=(1/sin²α)·(sinα/cosα)/[(sin/cosα)+(cosα/sinα)]=
=[1/(sinαcosα)]·(sinαcosα)/(sin²α+cos²α)=
=1/1=1;
6)[(1-ctgβ)/(1-tgβ)]·tgβ=[(1-cosβ/sinβ)/(1-sinβ/cosβ)]·tgβ=
=[(sinβ-cosβ)/sinβ]/[(cosβ-sinβ)/cosβ]·tgβ=
= -(cosβ/sinβ)·tgβ=-ctgβ·tgβ=-1;
=4tgα·ctgα=4;
2)tgα/(1+tg²α) -ctgα/(1+ctg²α)=tgα/(1/cos²α)-ctgα/(1/sin²α)=
=tgα·cos²α-ctgα·sin²α=(sinα/cosα)·cos²α-(cosα/sinα)·sin²α=
=sinαcosα-sinαcosα=0;
3)1/(1+tg²α)+1/(1+ctg²α)=1/(1/cos²α)+1/(1/sin²α)=
=cos²α+sin²α=1;
4)ctg²α-cos²α-ctg²α·cos²α=ctg²α-cos²α(1+ctg²α)=
=ctg²α-cos²α·(1/sin²α)=ctg²α-ctg²α=0;
5)[(1+ctg²α)/(tgα+ctgα)]·tgα=(1/sin²α)·(sinα/cosα)/[(sin/cosα)+(cosα/sinα)]=
=[1/(sinαcosα)]·(sinαcosα)/(sin²α+cos²α)=
=1/1=1;
6)[(1-ctgβ)/(1-tgβ)]·tgβ=[(1-cosβ/sinβ)/(1-sinβ/cosβ)]·tgβ=
=[(sinβ-cosβ)/sinβ]/[(cosβ-sinβ)/cosβ]·tgβ=
= -(cosβ/sinβ)·tgβ=-ctgβ·tgβ=-1;
Приложения:

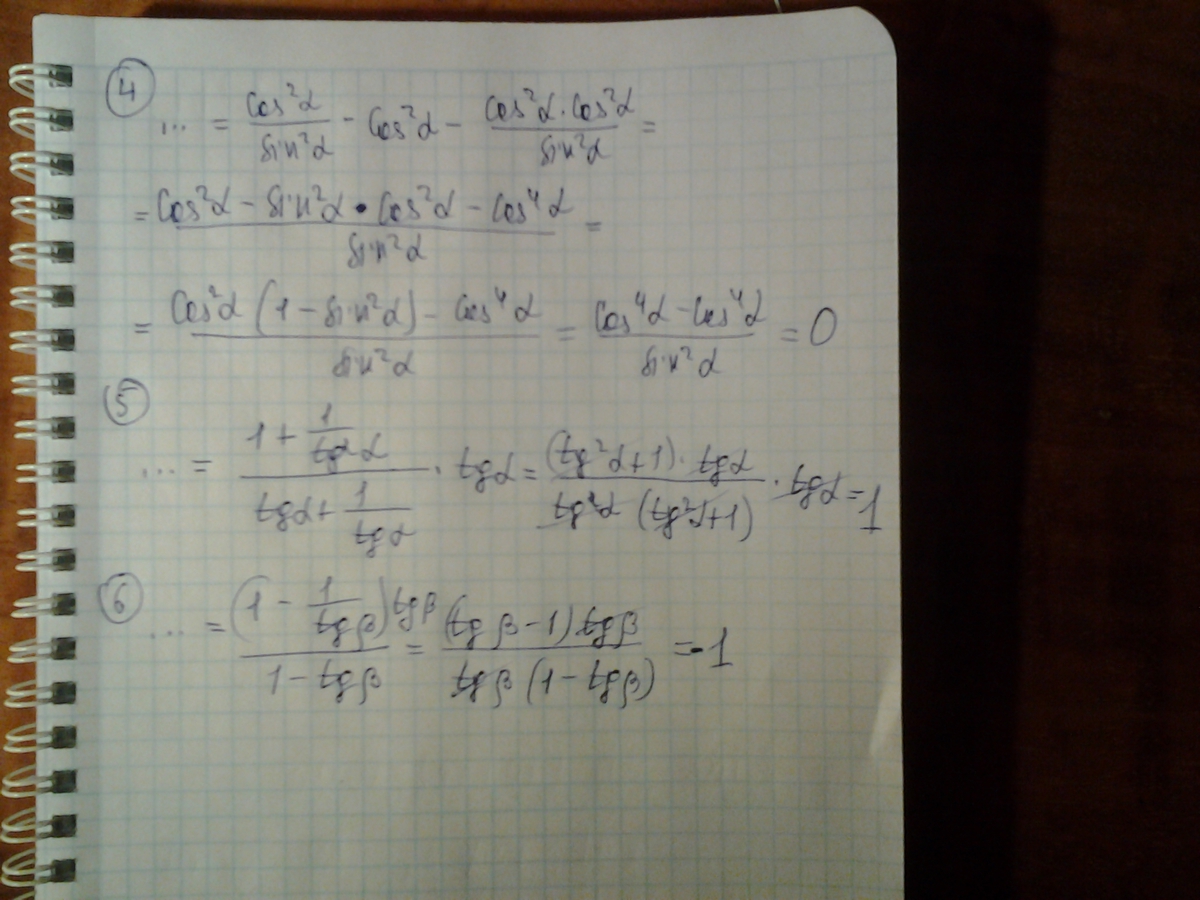
Похожие вопросы
Предмет: Литература,
автор: nvxlt
Предмет: Математика,
автор: arkasha001
Предмет: Алгебра,
автор: MilanaStar167
Предмет: Биология,
автор: maksimkrzhemin
Предмет: История,
автор: almonlina15