Предмет: Геометрия,
автор: darya280797
Помогите,пожалуйста с задачами по геометрии,задание во вложении.
Приложения:

Ответы
Автор ответа:
0
Попробую, хотя я не люблю геометрию.
1) Длины дуг относятся как 3 : 5, пусть их длины равны 3x и 5x.
Длина окружности C = 2pi*R = 8x
x = pi/4*R
L(AB) = pi*R*a/180 (где а - это угол дуги) = 3x = 3pi/4*R
a = AOB = 3/4*180 = 135°
L(BMA) = pi*R*b/180 = 5x = 5pi/4*R
b = 5/4*180 = 225°
Угол OBC = 90° (радиус всегда перпендикулярен к касательной).
Треугольник AOB - равнобедренный, поэтому
угол OBA = (180° - 135°)/2 = 45°/2 = 22,5°
Угол ABC = 90° - 22,5° = 67,5°
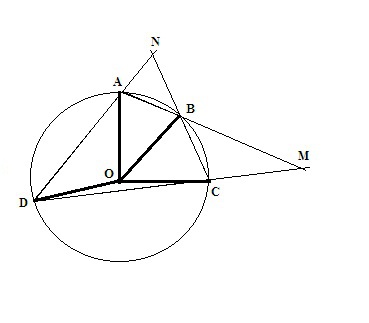
2) Окружность состоит из частей длиной 2, 3, 9 и 6.
Я ее изобразил на 1 рисунке. Требуется найти углы ANB и BMC.
Длина окр. C = 2pi*R = (2+3+9+6)*x = 20x
x = pi/10*R
Длины дуг: AB = 2x = 2pi/10*R; BC = 3x = 3pi/10*R; CD = 9x = 9pi/10*R;
DA = 6x = 6pi/10*R
Углы: AOB = 2pi/10 = 36°; BOC = 3pi/10 = 54°; COD = 9pi/10 = 162°;
DOA = 6pi/10 = 108° .
Заметим, что AOC = AOB + BOC = 36° + 54° = 90°
В треугольнике ANB углы NAB + ABN + ANB = 180°
Треугольники внутри круга все равнобедренные, поэтому:
OAB = OBA = (180° - AOB)/2 = (180° - 36°)/2 = 72°
OAD = ODA = (180° - DOA)/2 = (180° - 108°)/2 = 36°
ODC = OCD = (180° - COD)/2 = (180° - 162°)/2 = 9°
OCB = OBC = (180° - BOC)/2 = (180° - 54°)/2 = 63°
Угол NAD = 180° = NAB + OAB + OAD
NAB = 180° - OAB - OAD = 180° - 72° - 36° = 72°
Угол NBC = 180° = NBA + OBA + OBC
NBA = 180° - OBA - OBC = 180° - 72° - 63° = 45°
Угол MCD = 180° = MCB + OCB + OCD
MCB = 180° - OCB - OCD = 180° - 63° - 9° = 108°
Угол MBC = NBA = 45°, потому что это вертикальные углы.
Наконец, добрались до главных углов:
CMB = 180° - MBC - MCB = 180° - 45° - 108° = 27°
ANB = 180° - NBA - NAB = 180° - 45° - 72° = 63°
Главное - внимательно следить за углами, что с чем складывается.
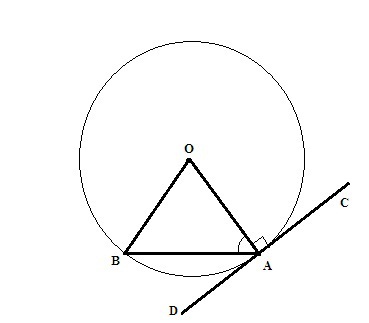
3) Эту задачу я изобразил на рисунке 2.
Она намного проще.
Угол OAC = OAD = 90° (касательная перпендикулярна к радиусу)
Треугольник AOB - равносторонний (AB = AO = OB = R)
Угол OAB = 60°
Угол между хордой и касательной
BAD = OAD - OAB = 90° - 60° = 30°
1) Длины дуг относятся как 3 : 5, пусть их длины равны 3x и 5x.
Длина окружности C = 2pi*R = 8x
x = pi/4*R
L(AB) = pi*R*a/180 (где а - это угол дуги) = 3x = 3pi/4*R
a = AOB = 3/4*180 = 135°
L(BMA) = pi*R*b/180 = 5x = 5pi/4*R
b = 5/4*180 = 225°
Угол OBC = 90° (радиус всегда перпендикулярен к касательной).
Треугольник AOB - равнобедренный, поэтому
угол OBA = (180° - 135°)/2 = 45°/2 = 22,5°
Угол ABC = 90° - 22,5° = 67,5°
2) Окружность состоит из частей длиной 2, 3, 9 и 6.
Я ее изобразил на 1 рисунке. Требуется найти углы ANB и BMC.
Длина окр. C = 2pi*R = (2+3+9+6)*x = 20x
x = pi/10*R
Длины дуг: AB = 2x = 2pi/10*R; BC = 3x = 3pi/10*R; CD = 9x = 9pi/10*R;
DA = 6x = 6pi/10*R
Углы: AOB = 2pi/10 = 36°; BOC = 3pi/10 = 54°; COD = 9pi/10 = 162°;
DOA = 6pi/10 = 108° .
Заметим, что AOC = AOB + BOC = 36° + 54° = 90°
В треугольнике ANB углы NAB + ABN + ANB = 180°
Треугольники внутри круга все равнобедренные, поэтому:
OAB = OBA = (180° - AOB)/2 = (180° - 36°)/2 = 72°
OAD = ODA = (180° - DOA)/2 = (180° - 108°)/2 = 36°
ODC = OCD = (180° - COD)/2 = (180° - 162°)/2 = 9°
OCB = OBC = (180° - BOC)/2 = (180° - 54°)/2 = 63°
Угол NAD = 180° = NAB + OAB + OAD
NAB = 180° - OAB - OAD = 180° - 72° - 36° = 72°
Угол NBC = 180° = NBA + OBA + OBC
NBA = 180° - OBA - OBC = 180° - 72° - 63° = 45°
Угол MCD = 180° = MCB + OCB + OCD
MCB = 180° - OCB - OCD = 180° - 63° - 9° = 108°
Угол MBC = NBA = 45°, потому что это вертикальные углы.
Наконец, добрались до главных углов:
CMB = 180° - MBC - MCB = 180° - 45° - 108° = 27°
ANB = 180° - NBA - NAB = 180° - 45° - 72° = 63°
Главное - внимательно следить за углами, что с чем складывается.
3) Эту задачу я изобразил на рисунке 2.
Она намного проще.
Угол OAC = OAD = 90° (касательная перпендикулярна к радиусу)
Треугольник AOB - равносторонний (AB = AO = OB = R)
Угол OAB = 60°
Угол между хордой и касательной
BAD = OAD - OAB = 90° - 60° = 30°
Приложения:
Похожие вопросы
Предмет: Математика,
автор: tatianadavid7623
Предмет: Химия,
автор: aleksia58
Предмет: Математика,
автор: Kodzikk
Предмет: Физика,
автор: aflova
Предмет: Математика,
автор: nastayTIX