Предмет: Геометрия,
автор: acnetoris
в треугольнике abc угол c равен 90° ab=6, tga=2 на корень из 2. Найдите AC
Ответы
Автор ответа:
0
Если есть проблемы с отображением, смотрите снимок ответа, который приложен к нему.
====
Смотрите рисунок, приложенный к ответу.
Рассмотрим . Из условия ясно, что он — прямоугольный (так как
. Из условия ясно, что он — прямоугольный (так как  ).
).  — гипотенуза,
— гипотенуза,  — искомый катет,
— искомый катет, 
Тангенс острого угла прямоугольного треугольника есть отношение противолежащего катета к прилежащему катету. То есть:
Отсюда:
Как видим, оба катета неизвестны. Но есть выход — теорема Пифагора. Покажем теорему Пифагора для данного треугольника:

Как мы выяснили чуть выше .
.
Заменяем и получаем:

Немного поколдуем:

Отсюда найдем :
:

Теперь напомню зачем нам нужно было

Подставляем вместо новую подстановку:
новую подстановку:

Отлично. В формуле для нахождения ответа не осталось ни одной неизвестной. Подставляем то, что есть в формуле. Из условия:

Найдем, наконец,


Это ответ.
====
Смотрите рисунок, приложенный к ответу.
Рассмотрим
Тангенс острого угла прямоугольного треугольника есть отношение противолежащего катета к прилежащему катету. То есть:
Отсюда:
Как видим, оба катета неизвестны. Но есть выход — теорема Пифагора. Покажем теорему Пифагора для данного треугольника:
Как мы выяснили чуть выше
Заменяем и получаем:
Немного поколдуем:
Отсюда найдем
Теперь напомню зачем нам нужно было
Подставляем вместо
Отлично. В формуле для нахождения ответа не осталось ни одной неизвестной. Подставляем то, что есть в формуле. Из условия:
Найдем, наконец,
Это ответ.
Приложения:
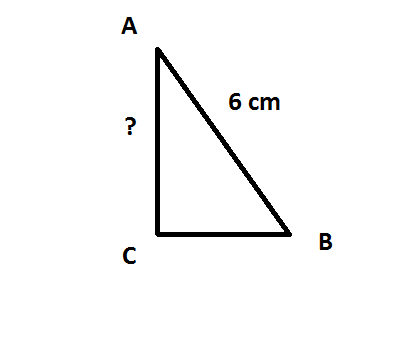

Похожие вопросы
Предмет: Геометрия,
автор: letsartur211123
Предмет: Биология,
автор: teawithmilk8
Предмет: Алгебра,
автор: vikakorkhov78
Предмет: Литература,
автор: dolmatika
Предмет: Литература,
автор: Нася0009