Предмет: Геометрия,
автор: BJIADA
Основания трапеции равны 4 и 16. Найдите радиусы окружностей, вписанной в трапецию и описанной около неё, если известно, что эти окружности существуют.
С рисунком.
Ответы
Автор ответа:
0
Решение дано во вложении.
Приложения:
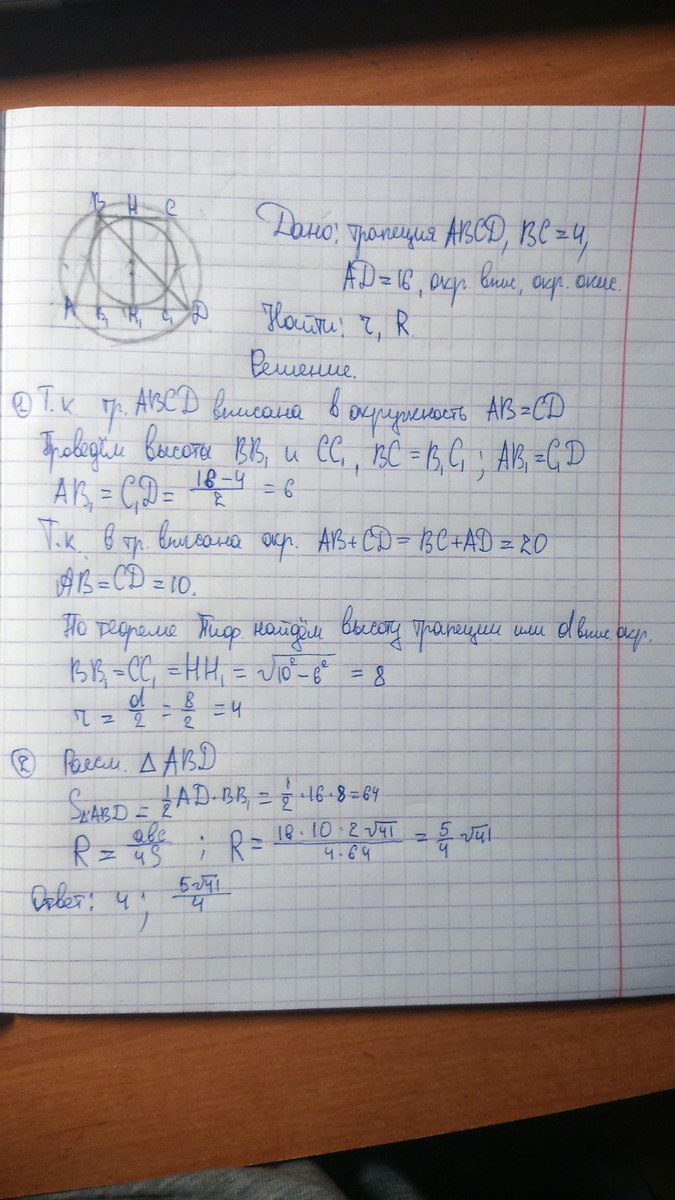
Автор ответа:
0
Спасибо!)
Автор ответа:
0
Пожалуйста, давайте еще))
Автор ответа:
0
Так как вписанная и описанная окружности существуют, то данная трапеция равнобедренной.
По свойства описанного четырехугольника, суммы его противоположных сторон равны:

Две стороны AD и ВС известны, две другие АВ и СD равны между собой, тогда:

Проведем высоты BH и СК, равные диаметру вписанной окружности. Тогда отрезок НК будет равен отрезку ВС, а оставшаяся длина отрезка АD распределится поровну между отрезками АН и КD. Получаем:
 ;
; 
Рассмотрим треугольник АВН. По теореме Пифагора:

Так как найден диаметр вписанной окружности, то можно найти и радиус:

Проведем диагональ трапеции AC. По теореме Пифагора для треугольника АСК получим:

Рассмотрим треугольник АСD. Окружности, описанные около заданной трапеции и около треугольника ACD совпадают. Тогда найдем радиус описанной окружности треугольника ACD через теорему синусов: отношение стороны треугольника к синусу противолежащего угла есть удвоенный радиус описанной окружности. Удобно записать соотношение в следующем виде:

Неизвестный синус найдем из прямоугольного треугольника АКС:

Выражаем R и подставляем выражение для синуса:

Ответ: радиус вписанной окружности ; радиус описанной окружности
; радиус описанной окружности 
По свойства описанного четырехугольника, суммы его противоположных сторон равны:
Две стороны AD и ВС известны, две другие АВ и СD равны между собой, тогда:
Проведем высоты BH и СК, равные диаметру вписанной окружности. Тогда отрезок НК будет равен отрезку ВС, а оставшаяся длина отрезка АD распределится поровну между отрезками АН и КD. Получаем:
Рассмотрим треугольник АВН. По теореме Пифагора:
Так как найден диаметр вписанной окружности, то можно найти и радиус:
Проведем диагональ трапеции AC. По теореме Пифагора для треугольника АСК получим:
Рассмотрим треугольник АСD. Окружности, описанные около заданной трапеции и около треугольника ACD совпадают. Тогда найдем радиус описанной окружности треугольника ACD через теорему синусов: отношение стороны треугольника к синусу противолежащего угла есть удвоенный радиус описанной окружности. Удобно записать соотношение в следующем виде:
Неизвестный синус найдем из прямоугольного треугольника АКС:
Выражаем R и подставляем выражение для синуса:
Ответ: радиус вписанной окружности
Приложения:

Похожие вопросы
Предмет: История,
автор: hffhgfyggfg
Предмет: Геометрия,
автор: Аноним
Предмет: Геометрия,
автор: milanakrivoseeva0
Предмет: Литература,
автор: Тамаз1
Предмет: Информатика,
автор: ravenkova