Предмет: Математика,
автор: kurmeisgloktarugar
Решите параметр пжалста :)
Приложения:
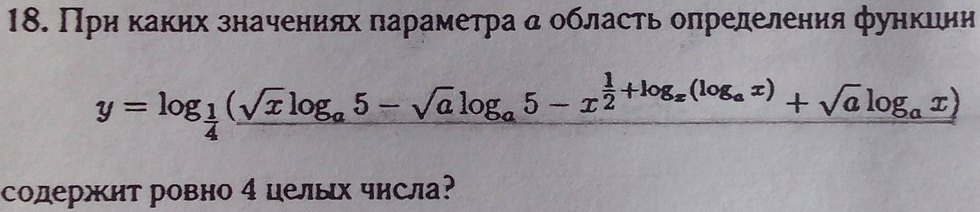
Ответы
Автор ответа:
0
Область определени для а: a ∈ (0; 1) U (1; +oo)
Область определени для x: x ∈ (0; 1) U (1; +oo)
Выражение под логарифмом должно быть положительно

Попробуем упростить

Известно, что , поэтому
, поэтому

Выносим за скобки одинаковые множители

Раскладываем на множители

Разность логарифмов равна логарифму от дроби

Произведение положительно, если знаки множителей одинаковы.
1) Если a ∈ (0; 1), то log_a (5/x) - функция убывающая
а) Пусть оба множителя отрицательны.
{ √x - √a < 0
{ log_a (5/x) < 0
Получаем
{ 0 < x < a < 1
{ 5/x > 1; x < 5
Тогда х вообще не принимает целых значений. Не подходит
б) Пусть оба множителя положительны
{ √x - √a > 0
{ log_a (5/x) > 0
Получаем
{ x > a
{ 5/x < 1; x > 5 > a
При 0 < a < 1 будет бесконечное множество целых x > 5
2) Если a > 1, то функция log_a (5/x) - возрастающая.
а) Пусть множители отрицательны
{ √x - √a < 0
{ log_a (5/x) < 0
Получаем
{ x < a
{ 0 < 5/x < 1; x > 5
При а = 10 будет 4 целых значения x: 6, 7, 8, 9
б) Пусть множители положительны
{ √x - √a > 0
{ log_a (5/x) > 0
Получаем
{ x > a > 1
{ 5/x > 1; x < 5
Здесь только 3 целых значения x: 2, 3, 4.
Ответ: a = 10
Область определени для x: x ∈ (0; 1) U (1; +oo)
Выражение под логарифмом должно быть положительно
Попробуем упростить
Известно, что
Выносим за скобки одинаковые множители
Раскладываем на множители
Разность логарифмов равна логарифму от дроби
Произведение положительно, если знаки множителей одинаковы.
1) Если a ∈ (0; 1), то log_a (5/x) - функция убывающая
а) Пусть оба множителя отрицательны.
{ √x - √a < 0
{ log_a (5/x) < 0
Получаем
{ 0 < x < a < 1
{ 5/x > 1; x < 5
Тогда х вообще не принимает целых значений. Не подходит
б) Пусть оба множителя положительны
{ √x - √a > 0
{ log_a (5/x) > 0
Получаем
{ x > a
{ 5/x < 1; x > 5 > a
При 0 < a < 1 будет бесконечное множество целых x > 5
2) Если a > 1, то функция log_a (5/x) - возрастающая.
а) Пусть множители отрицательны
{ √x - √a < 0
{ log_a (5/x) < 0
Получаем
{ x < a
{ 0 < 5/x < 1; x > 5
При а = 10 будет 4 целых значения x: 6, 7, 8, 9
б) Пусть множители положительны
{ √x - √a > 0
{ log_a (5/x) > 0
Получаем
{ x > a > 1
{ 5/x > 1; x < 5
Здесь только 3 целых значения x: 2, 3, 4.
Ответ: a = 10
Автор ответа:
0
a=(9;10}, но ты молодец :D
Похожие вопросы
Предмет: Математика,
автор: onigiri11168
Предмет: Английский язык,
автор: wuxu
Предмет: Математика,
автор: marsel113
Предмет: Математика,
автор: LucasRossi
Предмет: Обществознание,
автор: NightyMigly