Предмет: Алгебра,
автор: Vasilisa1996
решить определенный интеграл
Приложения:
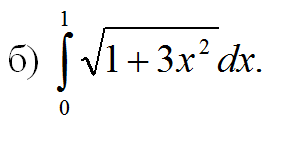
Ответы
Автор ответа:
0
Тригонометрическая постановка
x=tgt/√3, тогда 1+x²=1+tg²t=1/cos²t
dx=dt/√3cos²t
если х=0 tgt=0 t=0
если x=1, значит tgt=√3, t=π/3
![intlimits^1_0 { sqrt{1+3x^2} } , dx = intlimits^{ frac{ pi }{3}} _0 { frac{1}{ sqrt{3}cos^3x } } , dx=[1=cos^2x+sin^2x]= intlimits^{ frac{ pi }{3}} _0 { frac{cos^2x+sin^2x}{ sqrt{3}cos^3x } } , dx intlimits^1_0 { sqrt{1+3x^2} } , dx = intlimits^{ frac{ pi }{3}} _0 { frac{1}{ sqrt{3}cos^3x } } , dx=[1=cos^2x+sin^2x]= intlimits^{ frac{ pi }{3}} _0 { frac{cos^2x+sin^2x}{ sqrt{3}cos^3x } } , dx](https://tex.z-dn.net/?f=+intlimits%5E1_0+%7B+sqrt%7B1%2B3x%5E2%7D+%7D+%2C+dx+%3D+intlimits%5E%7B+frac%7B+pi+%7D%7B3%7D%7D+_0+%7B+frac%7B1%7D%7B+sqrt%7B3%7Dcos%5E3x+%7D+%7D+%2C+dx%3D%5B1%3Dcos%5E2x%2Bsin%5E2x%5D%3D++intlimits%5E%7B+frac%7B+pi+%7D%7B3%7D%7D+_0+%7B+frac%7Bcos%5E2x%2Bsin%5E2x%7D%7B+sqrt%7B3%7Dcos%5E3x+%7D+%7D+%2C+dx)

Первый интеграл- есть в таблице, второй интеграл от дроби.
Или по формуле интегрирования по частям:
u=√(1+3x²); dv=dx
x=tgt/√3, тогда 1+x²=1+tg²t=1/cos²t
dx=dt/√3cos²t
если х=0 tgt=0 t=0
если x=1, значит tgt=√3, t=π/3
Первый интеграл- есть в таблице, второй интеграл от дроби.
Или по формуле интегрирования по частям:
u=√(1+3x²); dv=dx
Похожие вопросы
Предмет: Математика,
автор: ratmirasmatullayev
Предмет: Математика,
автор: nikitaktoto9
Предмет: Геометрия,
автор: Аноним
Предмет: Химия,
автор: armenoganesyan
Предмет: Алгебра,
автор: hockeylove