Предмет: Алгебра,
автор: dkdjkfd
Объясните как преобразовали !!! Пожалуйста, можете расписать решение
Приложения:
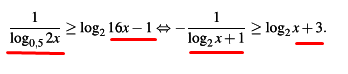
Ответы
Автор ответа:
0
- - +
_____________[-2]__________(-1)___________
t∈(-∞;-1)
log₂x<-1 ОДЗ: x>0
log₂x<log₂(1/2)
2- основание логарифма, 2>1, следовательно
x<1/2
С учётом ОДЗ получаем 0<x<1/2
Ответ: (0; 1/2)
Автор ответа:
0
решение смотри во вложении
Приложения:

Автор ответа:
0
и как это из неравенства получилось уравнение?
Автор ответа:
0
числитель не может быть < 0
Автор ответа:
0
уравнение то никак из этого не получится))
Автор ответа:
0
зато знаменатель может быть < 0
Автор ответа:
0
так оно и есть
Похожие вопросы
Предмет: Химия,
автор: kornevadasa5
Предмет: Литература,
автор: kuprikovasvetlana39
Предмет: Физика,
автор: lilshy
Предмет: Алгебра,
автор: KristinaKLeb
Предмет: Математика,
автор: ЖЕНЯ4653