Предмет: Алгебра,
автор: Ксения2050
Помогите пожалуйстааа
Приложения:
Ответы
Автор ответа:
0
Решение
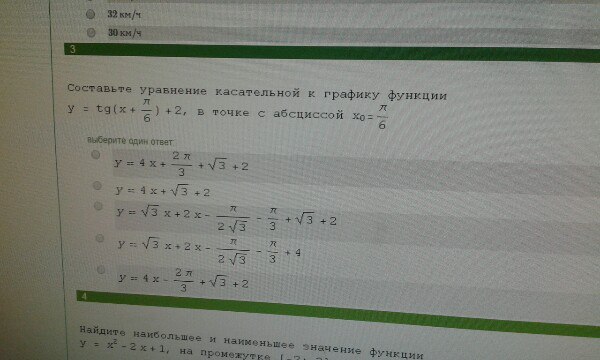
y = tg(x+π/6)+2 в точке с абсциссой x₀ = π/6.
Запишем уравнение касательной в общем виде:
y = y₀ + y'(x₀)(x - x₀)
По условию задачи x₀ = π/6, тогда:
y₀ = tg(π/6 + π/6) + 2 = tg(π/3) + 2 = √3 + 2
y₀ = √3 + 2
Теперь найдем производную:
y ` = tg²(x + π/6) + 1
следовательно:
f'(π/6) = tg²(π/6+π/6) + 1 = 4
В результате имеем:
y = √3 + 2 + 4*(x - π/6) = √3 + 2 + 4x - 2π/3
y = 4x - 2π/3 + √3 + 2 - искомое уравнение касательной
y = tg(x+π/6)+2 в точке с абсциссой x₀ = π/6.
Запишем уравнение касательной в общем виде:
y = y₀ + y'(x₀)(x - x₀)
По условию задачи x₀ = π/6, тогда:
y₀ = tg(π/6 + π/6) + 2 = tg(π/3) + 2 = √3 + 2
y₀ = √3 + 2
Теперь найдем производную:
y ` = tg²(x + π/6) + 1
следовательно:
f'(π/6) = tg²(π/6+π/6) + 1 = 4
В результате имеем:
y = √3 + 2 + 4*(x - π/6) = √3 + 2 + 4x - 2π/3
y = 4x - 2π/3 + √3 + 2 - искомое уравнение касательной
Похожие вопросы
Предмет: Английский язык,
автор: davudik2999
Предмет: Математика,
автор: daradaskevic911
Предмет: Немецкий язык,
автор: vabykovskaya
Предмет: Алгебра,
автор: Akula17
Предмет: Алгебра,
автор: nikitamihei