Question

Переходя к полярным координатам, найти площадь, ограниченную линиями:
x^2 + y^2 = 2x, x^2 + y^2 = 4x, y = x, y = 0 .

Answer 1

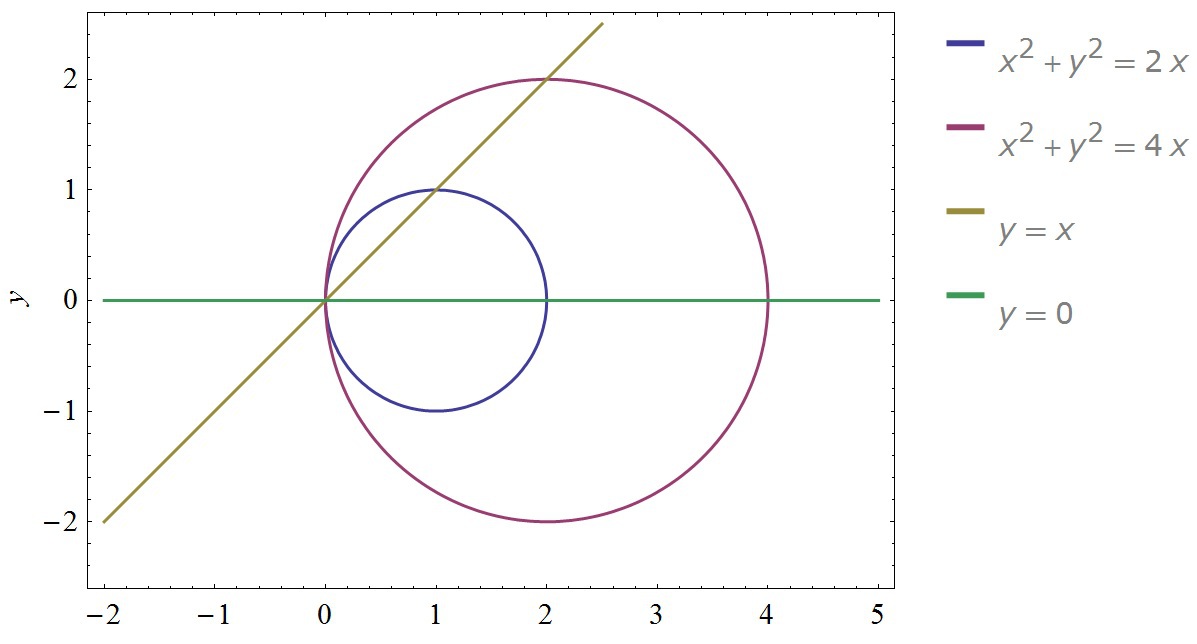
1) Строим фигуру.
$x^{2}+y^2=2x$
$x^2-2x+1+y^2=1$
$(x-1)^2+(y-0)^2=1$
Первое уравнение даёт нам окружность с центром в точке [1,0] и единичным радиусом. Второе даёт нам вторую окружность, по аналогии с первым. Третья функция строится поточечно. Взяв любое значение x, получаем y и проводим прямую. Четвёртая прямая при любом x, даёт y=0.
Площадь фигуры рассчитывается по формуле $S= intlimits intlimits{dx} , dy$
При переходе к полярным координатам не забываем dxdy=rdrdφ
x=rcosφ
y=rsinφ
Берём первое уравнение $x^2+y^2-2x=0$ и осуществляем преобразование (rcosφ)²+(rsinφ)²-2(rcosφ)=0
Вспоминаем тригонометрическое тождество cosφ²+sinφ²=1 и применяем:
r²-2rcosφ=0
r-2cosφ=0
Ровно по такой же схеме преобразуем x²+y²=4x в r=4cosφ
Прямая y=x даёт нам изменение угла от 0 до π/4 в полярной системе координат, r же меняется от малой окружности до большей.
$intlimits^ frac{ pi }{4}_0 {} , d phi intlimits^{4cos phi}_{2cosphi} {r} , dr = intlimits^ frac{ pi }{4}_0 {6cos^{2}phi } , d phi =6 intlimits^ frac{ pi }{4}_0 {( frac{1}{2}cos(2phi)+ frac{1}{2} )} , d phi= frac{3(2+ pi )}{4}$