Предмет: Алгебра,
автор: Lebry1
На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через С. Найдите длину отрезка касательной, проведенной из точки B к этой окружности.
Приложения:
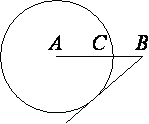
Ответы
Автор ответа:
0
Сначала ответ:  (то есть отрезок, который мы ищем) равен восьми. (См. мой прикреплённый рисунок).
(то есть отрезок, который мы ищем) равен восьми. (См. мой прикреплённый рисунок).
Теперь объясню, почему так, и алгоритм вычисления
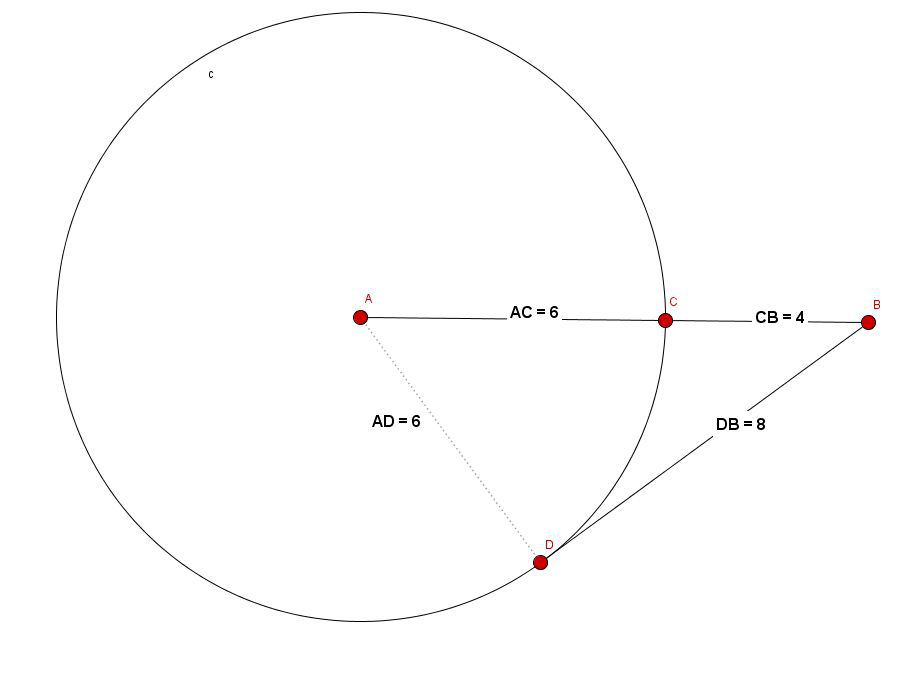
1. Поскольку центр окружности — A, а C — точка на окружности, то отрезок AC является радиусом.
2. Точка, в которой прямая касается окружности, тоже, очевидно, лежит на окружности, и поэтому AD — тоже радиус. Проводим пунктирную линию, чтобы посмотреть, что нам это даст.
3. А даёт вот что: теперь перед нами — прямоугольный треугольник, у которого один катет (AD) равен 6, а гипотенуза (AB) равна 10 (6+4).
4. Осталось только по теореме Пифагора вычислить второй катет:

Теперь объясню, почему так, и алгоритм вычисления
1. Поскольку центр окружности — A, а C — точка на окружности, то отрезок AC является радиусом.
2. Точка, в которой прямая касается окружности, тоже, очевидно, лежит на окружности, и поэтому AD — тоже радиус. Проводим пунктирную линию, чтобы посмотреть, что нам это даст.
3. А даёт вот что: теперь перед нами — прямоугольный треугольник, у которого один катет (AD) равен 6, а гипотенуза (AB) равна 10 (6+4).
4. Осталось только по теореме Пифагора вычислить второй катет:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ganetor778
Предмет: Математика,
автор: ayzadazhetkinshek
Предмет: Другие предметы,
автор: danalifena
Предмет: Физика,
автор: dasds
Предмет: Математика,
автор: nadeshda2008