Предмет: Алгебра,
автор: Cage7
Неопределенный интерграл
Приложения:
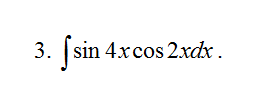
Ответы
Автор ответа:
0
∫sin4xcos2xdx=
по формуле произведения тригонометрических функций sinα на cosβ можно расписать интеграл как
∫1/2*(sin(4x-2x)+sin(4x+2x))dx=1/2∫(sin2x+sin(6x))dx=
или, используя свойства интеграла:
=1/2∫sin2xdx+1/2∫sin6xdx=
далее вводим замены:
t=2x, тогда dt=2dx dx=dt/2
k=6x, тогда dk=6dx dx=dk/6
=1/2∫1/2sin(t)dt+1/2∫1/6sin(k)dk=1/4(-cost)+1/12(-cos(k)=-1/4cos2x-1/12cos6x
по формуле произведения тригонометрических функций sinα на cosβ можно расписать интеграл как
∫1/2*(sin(4x-2x)+sin(4x+2x))dx=1/2∫(sin2x+sin(6x))dx=
или, используя свойства интеграла:
=1/2∫sin2xdx+1/2∫sin6xdx=
далее вводим замены:
t=2x, тогда dt=2dx dx=dt/2
k=6x, тогда dk=6dx dx=dk/6
=1/2∫1/2sin(t)dt+1/2∫1/6sin(k)dk=1/4(-cost)+1/12(-cos(k)=-1/4cos2x-1/12cos6x
Похожие вопросы
Предмет: Математика,
автор: pleasehelpmelol228
Предмет: Алгебра,
автор: danilstreltsov0676
Предмет: Другие предметы,
автор: sofiakey1
Предмет: Математика,
автор: барабакульна
Предмет: География,
автор: Даша565843957