Question

Хелп, плиз

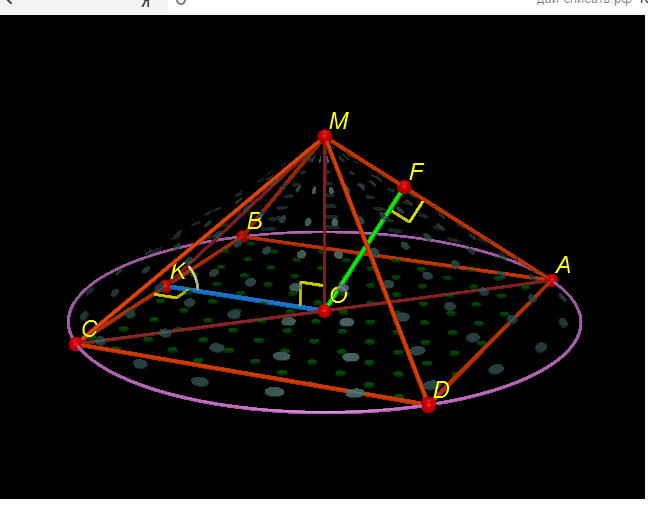
Конус описан около правильной четырехугольной пирамиды. Градусная мера угла наклона боковой грани пирамиды к плоскости основания равна 45 градусов.
Вычислите площадь осевого сечения конуса, если расстояние от центра основания пирамиды до образующей конуса равно 2 см

Answer 1

По условию $MABCD$ -  правильная четырехугольная пирамида, около которой описан конус 

$MO$ ⊥ $(ABC)$

∠ $MKO=45^circ$

$OF= 2$  см

Δ$AMC$  - осевое сечение конуса, где $AM$  и $MC$ - образующие конуса


Так как $MABCD$  - правильная четырехугольная пирамида,

значит в  основании лежит квадрат $ABCD$

$AC$ ∩ $BD=O$

$MO$ ⊥ $(ABC)$

Проведём $MK$  ⊥ $BC,$  тогда $OK$  ⊥ $BC$  и $textless MKO=45 ^circ$ как линейный угол двугранного угла 

$O$  - центр окружности, описанной около квадрата  

Значит расстояние от центра основания пирамиды до образующей конуса есть длина перпендикуляра  $OF$, т. е.  $OF$ ⊥ $AM$

Пусть $OK=KB=x,$  тогда $AB=2x$

$d=a sqrt{2}$,  где $d$ - диагональ квадрата, $a$ - сторона квадрата

$AC=BD=2 sqrt{2} x,$ ( как диагонали квадрата)

$AO=OC=OB=OD=x sqrt{2}$

Δ $MOK$ -  прямоугольный, равнобедренный,  следовательно $MO=x$

Рассмотрим Δ $MOA$ - прямоугольный
 
по теореме Пифагора найдем $MA= sqrt{MO^2+AO^2}= sqrt{x^2+(x sqrt{2})^2}= sqrt{ x^{2} +2x^2} = sqrt{3x^2} =x sqrt{3}$

С одной стороны:  $S_{MOA} = frac{1}{2} *MO*AO= frac{1}{2}*x*x sqrt{2} = frac{x^2 sqrt{2} }{2}$,

 а с другой стороны:  $S_{MOA}= frac{1}{2} *MA*OF= frac{1}{2}*x sqrt{3}*2=x sqrt{3}$
Приравняем:

$frac{x^2 sqrt{2} }{2} =x sqrt{3}$

$x sqrt{2} =2 sqrt{3}$

$x= frac{2 sqrt{3} }{ sqrt{2} }$

$x= sqrt{6}$

$OM= sqrt{6}$  см

Тогда $S_{AMC}= frac{1}{2}*MO*AC$

$AC=2AO=2 sqrt{2}x=2 sqrt{12} =4 sqrt{3}$  см

$S_{AMC}= frac{1}{2}* sqrt{6} *4 sqrt{3} =2 sqrt{18}=6 sqrt{2}$  (см ²)

Ответ:  $6 sqrt{2}$  см²