Предмет: Алгебра,
автор: dasha1176
27^sqrt х-7*9^+10*3^sqrt x=4
Ответы
Автор ответа:
0
Мне кажется, вы имели в виду, что
Примем
Тогда уравнение преобразуется к виду
Это кубическое уравнение. Одним из корней может быть делитель свободного члена. То есть делитель 4. Попробуем подставить 1 в уравнение.
Равенство выполняется. Значит - корень уравнения.
Остальные корни можно найти поделив многочлен на многочлен. То есть
поделить на
Во вложении показан алгоритм деления.
Как бы хорошо не знала бы ТЕХ, все равно картинки нужны :)))
В результате получается
Заметим, что по условию t - положительное число. При всех трех вариантах это условие выполняется.
1)
2)
Правая часть меньше 0, поэтому нет решения
3)
Ответ:
Приложения:
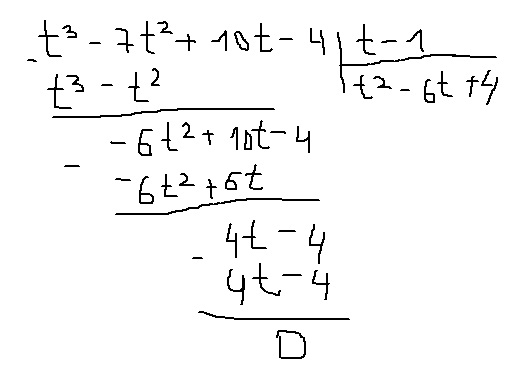
Похожие вопросы
Предмет: Русский язык,
автор: Crashixa
Предмет: Информатика,
автор: Queen141414
Предмет: Литература,
автор: eleonora475
Предмет: Химия,
автор: Lffc
Предмет: Математика,
автор: teamgak2