Question

Решите пожалуйста 2 задачки по геометрии.

ЕСЛИ МОЖНО ТО В ПОЛНОМ ТЕКСТЕ, а не в КРАТЦЕ.

И С РИСУНКОМ. 

СПАСИБО ЗАРАНЕЕ!!

Answer 1

1) Так как диагональ равна стороне. А все стороны у ромба равны, то его можно разделить на 2 равносторонних треугольника с углами по 60 градусов. Значит, углы ромба 60 градусов и 120 градусов.
2) Так как все стороны ромба равны, а их четыре - то P=10.5*4=42см 

Answer 2

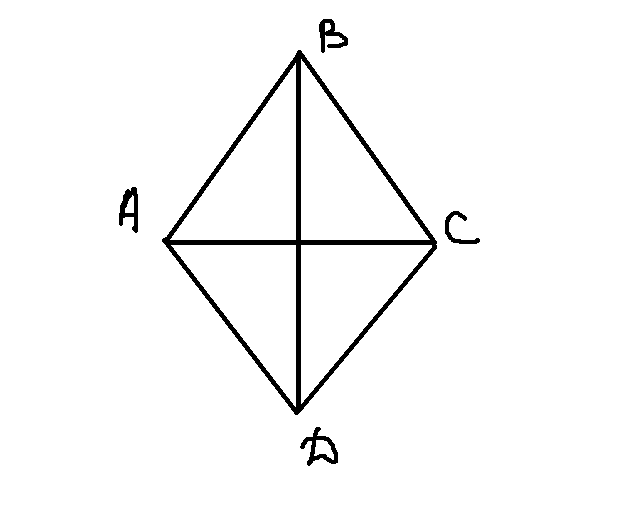
1. Дан ромб ABCD

AC - диагональ

AB - сторона

AB=AC

Найти

углы ромба

Решение

Диагональ AC делит ромб на два треугольника ABC и ADC

по условию AB=AC ⇒ ABC и ADC равносторонние треугольники

отсюда углы этих треугольников равны по 60 гр.

так же диагональ AC явл-ся биссектрисой углов A и С. ромба ABCD

След-но углы ромба равны: угол A=углу С = 60*2=120, и угол B = углу D = 60.

 

2.

Дан ромб ФИСВ

угол B=60

AC=10.5 см

Найти

P(abcd)-?

Решение:

в ромбе углы попарно равны: угол B = углу D и угол A=углу С

отсюда угол B = углу D = 60,  угол A=углу С= (180-60-60)/2 = 120

тк.к диагональ AС явл-ся биссектрисой углов A и С? соответственно углы образовавшихся треугольников ABC и ADC равны по 60 гр., а значит они равносторонние

⇒ сторона ромба = диагонали AC

P(abcd)=4*10.5=42 см