Предмет: Алгебра,
автор: ДжаджаБ
можно 2,3 пожалуйста)
Приложения:
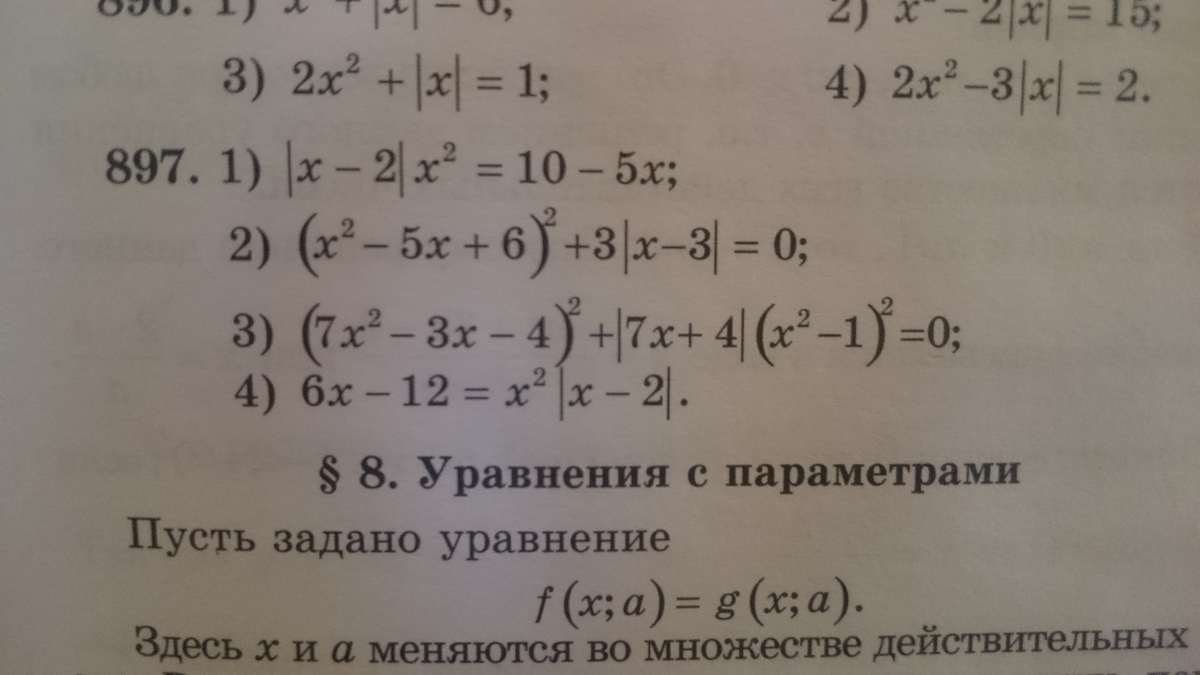
Ответы
Автор ответа:
0
Решение для 2 проще и я почти полностью изложил его ход в комментариях выше. Вот как я решал 3-й.
NB Возможно от вас требовалось в учебнике нечто другое, но из соображений лени я решил несколько сократить выкладки.
 (1)
(1)

Нечто в квадрате должно быть >=0 и модуль любой величины должен быть >=0. Значит, чтобы трансформированное равенство (1) выполнялось необходимо чтобы:
 (2)
(2)
Разбираемся с произведением справа
7x+4=0 или x²-1=0
т.е.

или

Проверяем. Находим нули скобки слева в (1)

Смотрим какие корни для правой и левой частей совпадают. Таких два:

2-й я решал так:

Проверяем скобку слева

Отлично. Получили один корень:
x=3
NB Возможно от вас требовалось в учебнике нечто другое, но из соображений лени я решил несколько сократить выкладки.
Нечто в квадрате должно быть >=0 и модуль любой величины должен быть >=0. Значит, чтобы трансформированное равенство (1) выполнялось необходимо чтобы:
Разбираемся с произведением справа
7x+4=0 или x²-1=0
т.е.
или
Проверяем. Находим нули скобки слева в (1)
Смотрим какие корни для правой и левой частей совпадают. Таких два:
2-й я решал так:
Проверяем скобку слева
Отлично. Получили один корень:
x=3
Похожие вопросы
Предмет: Математика,
автор: zannelermekovna
Предмет: Геометрия,
автор: Dilyara0910
Предмет: Математика,
автор: violettanazarenko201
Предмет: Физика,
автор: glebanch
Предмет: Информатика,
автор: Daniel090102