Предмет: Алгебра,
автор: kortniy
Помогите с тригонометрией)
Приложения:
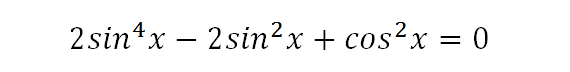
Ответы
Автор ответа:
0
2sin⁴x-2sin²x+cos²x=0
2sin⁴x-3sin²x+sin²x+cos²x=0
2sin⁴x-3sin²x+1=0 биквадратное тригонометрическое уравнение, замена переменной:
sin²x=t, t∈[0;1]
2t²-3t+1=0
t₁=1/2, t₂=1
обратная замена:

 ∈Z
∈Z




ответ:

n∈Z
2sin⁴x-3sin²x+sin²x+cos²x=0
2sin⁴x-3sin²x+1=0 биквадратное тригонометрическое уравнение, замена переменной:
sin²x=t, t∈[0;1]
2t²-3t+1=0
t₁=1/2, t₂=1
обратная замена:
ответ:
n∈Z
Похожие вопросы
Предмет: Биология,
автор: krapivin1205
Предмет: Математика,
автор: sanjarfifa
Предмет: История,
автор: lohhinedam
Предмет: Алгебра,
автор: Аноним