Question

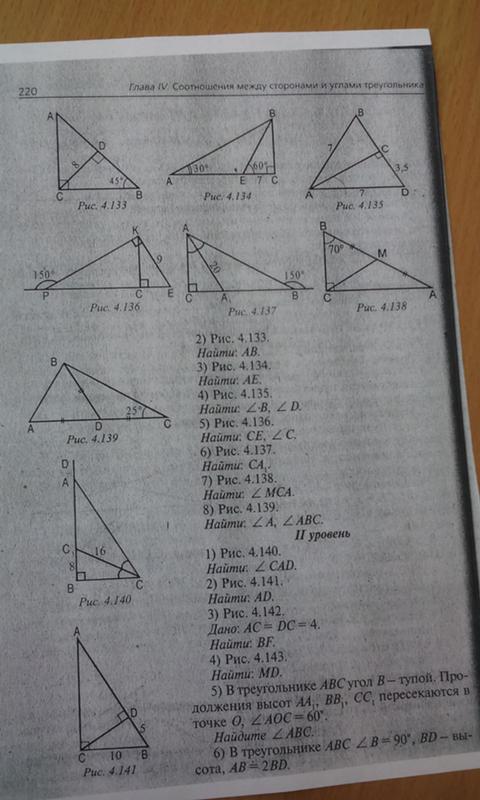
рис.4.136 и рис. 4.138
Помогите пожалуйста!

Answer 1

4.136

∠KPE = 30° (как смежный к углу 150°)

Из прямоугольного ΔPKE ∠KEP = 90° - ∠KPE = 90° - 30° = 60°

Из прямоугольного ΔKCE ∠CKE = 90° - ∠KEC = 90° - 60° = 30°

Из прямоугольного ΔKCE против угла в в 30° лежит половина гипотенузы ⇒ CE = KE / 2 = 9 / 2 = 4.5

∠PCK смежный с ∠KCE = 90° ⇒ ∠PCK = 90°

4.138

Из прямоугольного ΔABC ∠BAC = 90° - ∠ABC = 90° - 70° = 20°

Т.к. M - центр описанной окружности и CM = MA, то ΔCMA - равнобедренный и ∠MCA = ∠BAC = 20°

Answer 2

4.136. Угол С = 90°

Угол KPC = CKE = 180° - 150° = 30°.

Катет против угла 30° равен половине гипотенузы, поэтому

PE = KE*2 = 9*2 = 18

CE = KE/2 = 9/2 = 4,5.

4.138. CM медиана прямоугольного треугольника из прямого угла, она равна половине гипотенузы.

Треугольник ACM равнобедренный.

Угол MCA = MAC = 90° - 70° = 20°