Предмет: Алгебра,
автор: Ariana026
Помогите мне пожалуйста!
Найдите точки максимума по пунктам.вот этой функции
Приложения:
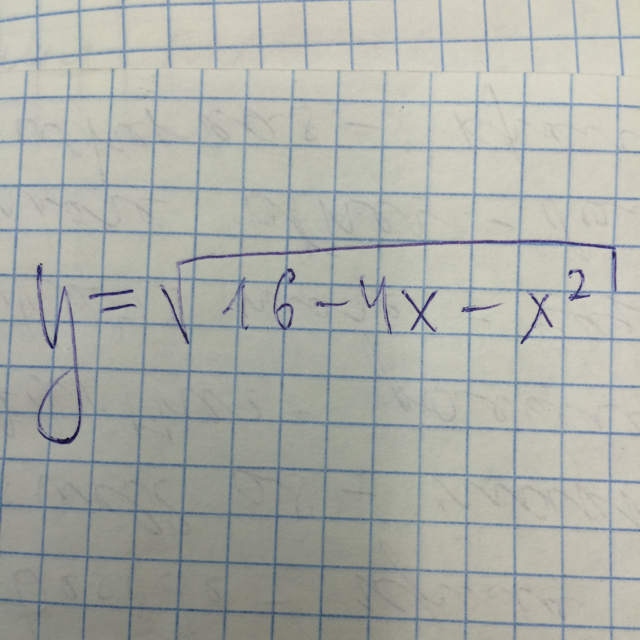
Ответы
Автор ответа:
0
Это задание нужно начинать решать с определения области определения: подкоренное выражение должно быть больше или равно нуля:
 ОДЗ= [ - 2 - 2sgr5; - 2 + 2sgr5 ]
ОДЗ= [ - 2 - 2sgr5; - 2 + 2sgr5 ]
Используем правило: производная
Производная будет следующей: ( - 4 - 2х) /
выполним вынесение множителя из числителя и сократим на 2
Получим
Найдём нули производной (признак критических точек)
Знаменатель дроби не может быть равен нулю, значит дробь равна нулю когда числитель обращается в ноль: - 2 - х = 0 =>х = - 2 - входит в ОДЗ и является точкой максимума (можно даже знаки не проверять. но если не верите:
Числовая прямая делиться точкой - 2 на два промежутка ( - 2 - 2sgr5; - 2] и [- 2; - 2 + 2sgr5)
Знаменатель производной всегда положительна, значит знак дроби зависит от знака числителя.
На первом промежутке производная имеет знак "+", на втором "-"
Что и требовалось доказать
Ответ: х = - 2 точка максимум
Используем правило: производная
Производная будет следующей: ( - 4 - 2х) /
выполним вынесение множителя из числителя и сократим на 2
Получим
Найдём нули производной (признак критических точек)
Знаменатель дроби не может быть равен нулю, значит дробь равна нулю когда числитель обращается в ноль: - 2 - х = 0 =>х = - 2 - входит в ОДЗ и является точкой максимума (можно даже знаки не проверять. но если не верите:
Числовая прямая делиться точкой - 2 на два промежутка ( - 2 - 2sgr5; - 2] и [- 2; - 2 + 2sgr5)
Знаменатель производной всегда положительна, значит знак дроби зависит от знака числителя.
На первом промежутке производная имеет знак "+", на втором "-"
Что и требовалось доказать
Ответ: х = - 2 точка максимум
Похожие вопросы
Предмет: Математика,
автор: kaaanakooosnik
Предмет: Геометрия,
автор: Sivacheva1612
Предмет: Қазақ тiлi,
автор: damirjaldybayev
Предмет: Математика,
автор: Srfenet