Предмет: Алгебра,
автор: rarararara5
Дано клеточное поле 2 × 3. Сколькими способами можно закрасить клетки этого поля так, чтобы никакие 2 закрашенные клетки не были соседними (по стороне)?
Ответы
Автор ответа:
0
1) По 1 клетке - 6 вариантов. Поскольку их всего одна, то никакие две не являются соседними.
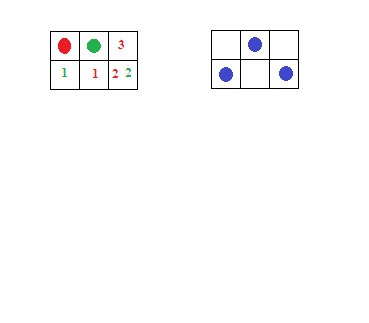
2) По 2 клетки. Если одна угловая (4 варианта), то вторую можно закрасить 3 способами. На 1 рис. Они обозначены красными.
Всего 12 вариантов.
3) По 2 клетки. Если одна в середине (2 варианта), то вторую можно закрасить 2 способами. На 1 рис. они обозначены зелеными.
Всего 4 варианта.
4) По 3 клетки - 2 варианта. Две в углах, третья на стороне.
На 2 рис. Они обозначены синими.
5) По 4 клетки - закрасить нельзя, обязательно будут соседи.
Итого 6 + 12 + 4 + 2 = 24 варианта.
2) По 2 клетки. Если одна угловая (4 варианта), то вторую можно закрасить 3 способами. На 1 рис. Они обозначены красными.
Всего 12 вариантов.
3) По 2 клетки. Если одна в середине (2 варианта), то вторую можно закрасить 2 способами. На 1 рис. они обозначены зелеными.
Всего 4 варианта.
4) По 3 клетки - 2 варианта. Две в углах, третья на стороне.
На 2 рис. Они обозначены синими.
5) По 4 клетки - закрасить нельзя, обязательно будут соседи.
Итого 6 + 12 + 4 + 2 = 24 варианта.
Приложения:
Автор ответа:
0
правильный ответ 17
Автор ответа:
0
Ну если убрать варианты по одной клетке, то останется 18. Но все равно - там четное количество должно быть. 17 не может.
Автор ответа:
0
Смотрите, это мое решение! Рассмотрим 2 серединные клетки. Если хотя бы одна из них занята, то закрашенными из оставшихся могут быть только 2 клетки, причем независимо друг от друга. В этом случае получается 2⋅2⋅2=8 вариантов. Если они не заняты, то для каждой оставшейся "доминошки" есть 3 варианта покраски - итого 3⋅3=9. Значит, всего вариантов по правилу суммы будет 8+9=17.
Автор ответа:
0
Возможно, у меня на 1 рисунке какие-то варианты будут повторяться. Если их оставить по 1, получится 17 разных. Я не проверял.
Автор ответа:
0
На 2 рисунке все четко. Один вариант - синие, второй вариант - пустые.
Похожие вопросы
Предмет: Английский язык,
автор: va6662920
Предмет: Русский язык,
автор: kariimm
Предмет: Математика,
автор: nurasyl1405
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: Аноним