Question

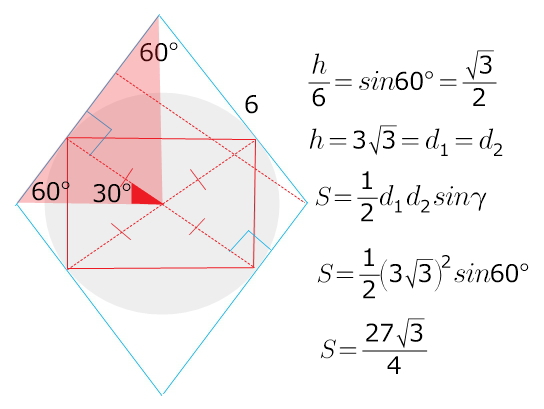
Дан ромб со стороной 6 и острым углом 60 градусов. Найдите площадь прямоугольника, вершины которого являются точками касания вписанной окружности со сторонами ромба.

Answer 1

прямоугольник --вписан в окружность))
его диагональ --диаметр окружности и высота ромба
проще всего найти его площадь как половину произведения диагоналей на синус угла между ними...
диагонали прямоугольника равны))
осталось оценить угол между ними...
центр вписанной в ромб окружности --это точка пересечения диагоналей ромба (которые являются биссектрисами его углов))
и в то же время --это точка пересечения диагоналей вписанного прямоугольника...