В правильной четырёхугольной пирамиде угол между противоположными боковыми гранями равен 40 градусам. Найдите угол наклона боковых граней к плоскости основания. Пожалуйста подробно
Ответы
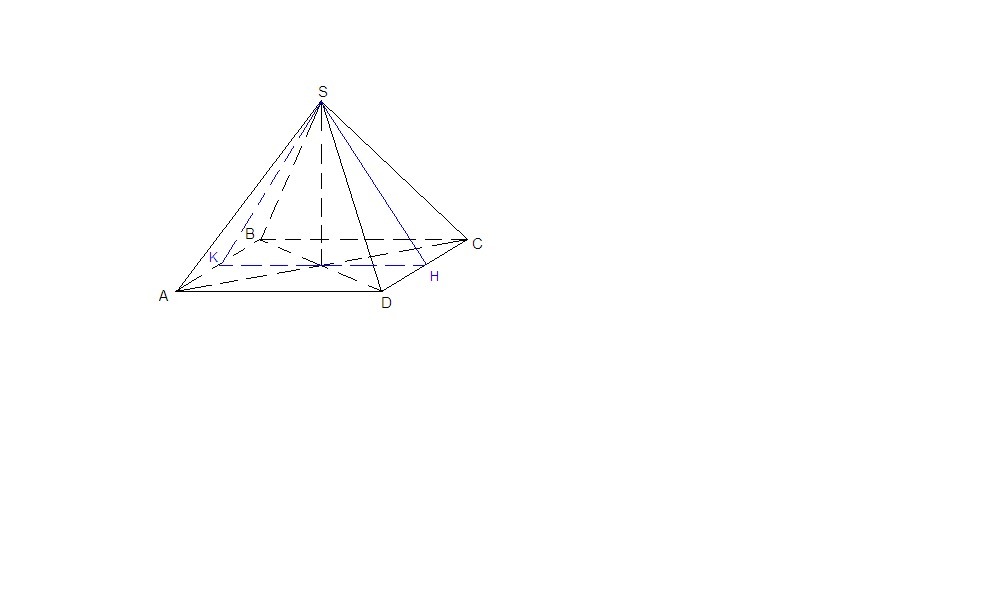
Проведем апофемы SK и SH в гранях SAB и SCD соответственно. ∠KSH = 40° - угол между противоположными боковыми гранями. Это можно доказать:
АВ║DC как стороны квадрата (пирамида правильная, значит в основании квадрат), значит АВ ║ SDC.
Плоскость SAB проходит через прямую АВ, параллельную SDC, и пересекает плоскость SDC, значит линия пересечения плоскостей параллельна АВ.
SK и SH перпендикулярны АВ, значит перпендикулярны и линии пересечения плоскостей. Тогда ∠KSH - линейный угол двугранного угла между плоскостями SAB и SDC.
Итак, ΔKSH - равнобедренный (апофемы равны), углы при основании равны:
∠SKH = ∠SHK = (180° - 40°)/2 = 70°
∠SHK - линейный угол двугранного угла между боковой гранью и плоскостью основания. Это тоже можно доказать:
KH ⊥ DC, так как КВСН прямоугольник (КВ = СН как половины равных сторон, КВ║СН так как лежат на противоположных сторонах квадрата, углы при вершинах С и В прямые),
SH ⊥DC как апофема, ⇒ ∠SHK - линейный угол двугранного угла между боковой гранью и плоскостью основания.
Все боковые грани наклонены под одним углом, так как пирамида правильная.
Ответ: 70°