Предмет: Математика,
автор: pasha1207
Решите пожалуйста срочно!!! Даю 25 баллов!!!!
1)
2)
3)
4)
5)
6)
Ответы
Автор ответа:
0
1.Пусть Log7 x=t тогда имеем t^2-2t-3=0 t[1]=3 t[2]=-1.
Делая обратную замену получаем:
Log7 x=3 х[1[=7^3, x[1]=343. x[2]=7^-1=1/7. x[2]=1/7
2,Т.к.0.2^0=1 и функция убывающая,то имеем
2x^2-x>0, x(2x-1)>0 x(x-0,5)>0
Ответ: (-∞;0) u (0.5;∞)
3.Посв-ву логарифмов имеем 2х+1 >х-2, х >-3.
Т.к.одз логарифмов х >2,то это и есть ответ.
4.Используем свойства степеней:
3^x*3^3+5*3^x/3=86
3^x(27+5/3)=86 3^x=86/(27+5/3), 3^x=86/(86/3)
3^x=3 , x=1-ответ.
5. Т.к. (1/2)^(-3)=8,тов нашем случае имеем 2х+5<8
2х<3< и х<1.5.По определению логарифма одз логарифма
2х>-5 х>-2.5
Тогда имеем ответ: -2.5< х<1.5
6.Имеем Log7 x + Log7 (х-1) > Log7 2
Используем св-во суммы логарифмов:
Log7 х (х-1) > Log7 2 или х(х-1)-2 > 0
х^2-х-2 > 0 или (х-2)(х+1) > 0 и учитывая одз неравенства х > 1
ответ х > 2
Ответ: х > 2
Делая обратную замену получаем:
Log7 x=3 х[1[=7^3, x[1]=343. x[2]=7^-1=1/7. x[2]=1/7
2,Т.к.0.2^0=1 и функция убывающая,то имеем
2x^2-x>0, x(2x-1)>0 x(x-0,5)>0
Ответ: (-∞;0) u (0.5;∞)
3.Посв-ву логарифмов имеем 2х+1 >х-2, х >-3.
Т.к.одз логарифмов х >2,то это и есть ответ.
4.Используем свойства степеней:
3^x*3^3+5*3^x/3=86
3^x(27+5/3)=86 3^x=86/(27+5/3), 3^x=86/(86/3)
3^x=3 , x=1-ответ.
5. Т.к. (1/2)^(-3)=8,тов нашем случае имеем 2х+5<8
2х<3< и х<1.5.По определению логарифма одз логарифма
2х>-5 х>-2.5
Тогда имеем ответ: -2.5< х<1.5
6.Имеем Log7 x + Log7 (х-1) > Log7 2
Используем св-во суммы логарифмов:
Log7 х (х-1) > Log7 2 или х(х-1)-2 > 0
х^2-х-2 > 0 или (х-2)(х+1) > 0 и учитывая одз неравенства х > 1
ответ х > 2
Ответ: х > 2
Автор ответа:
0
Применены: свойства логарифмов, метод интервалов, свойства степени
Приложения:
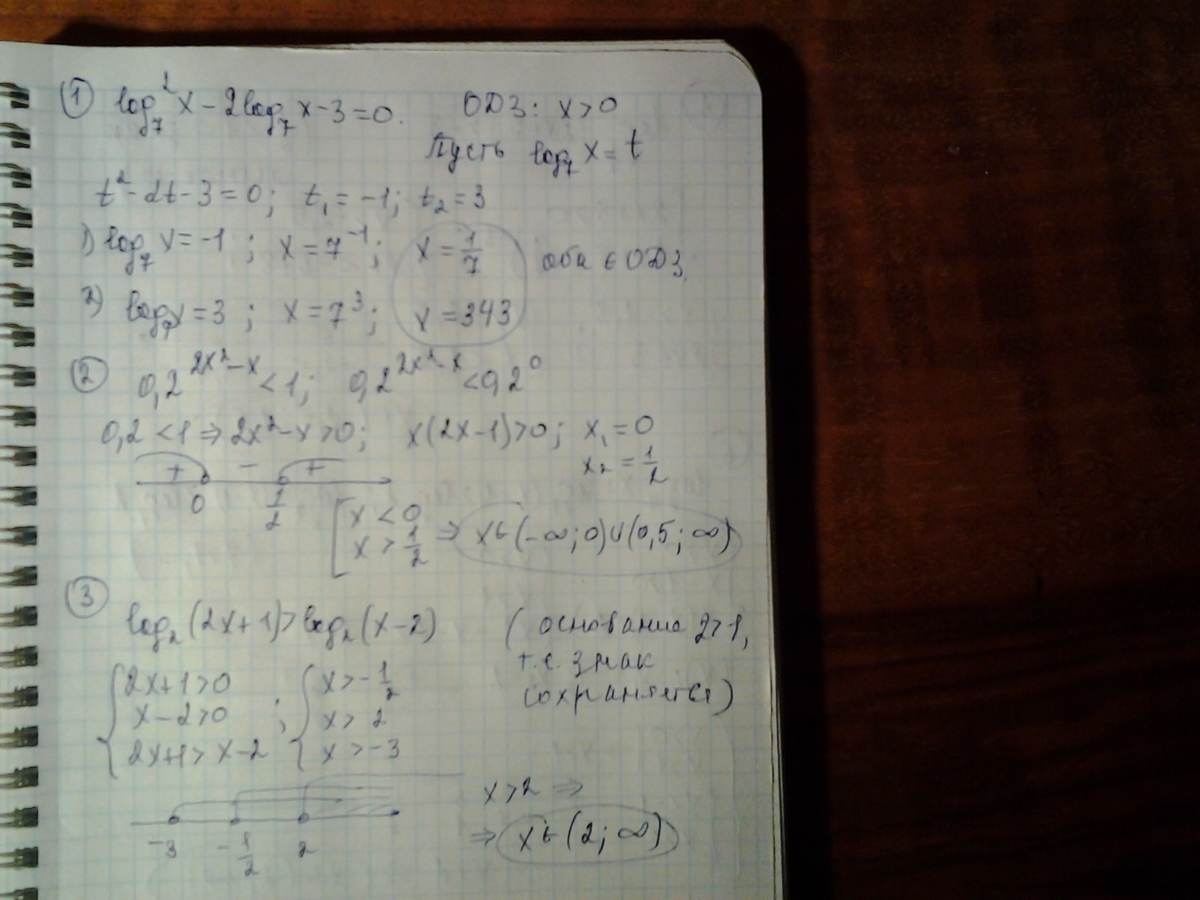
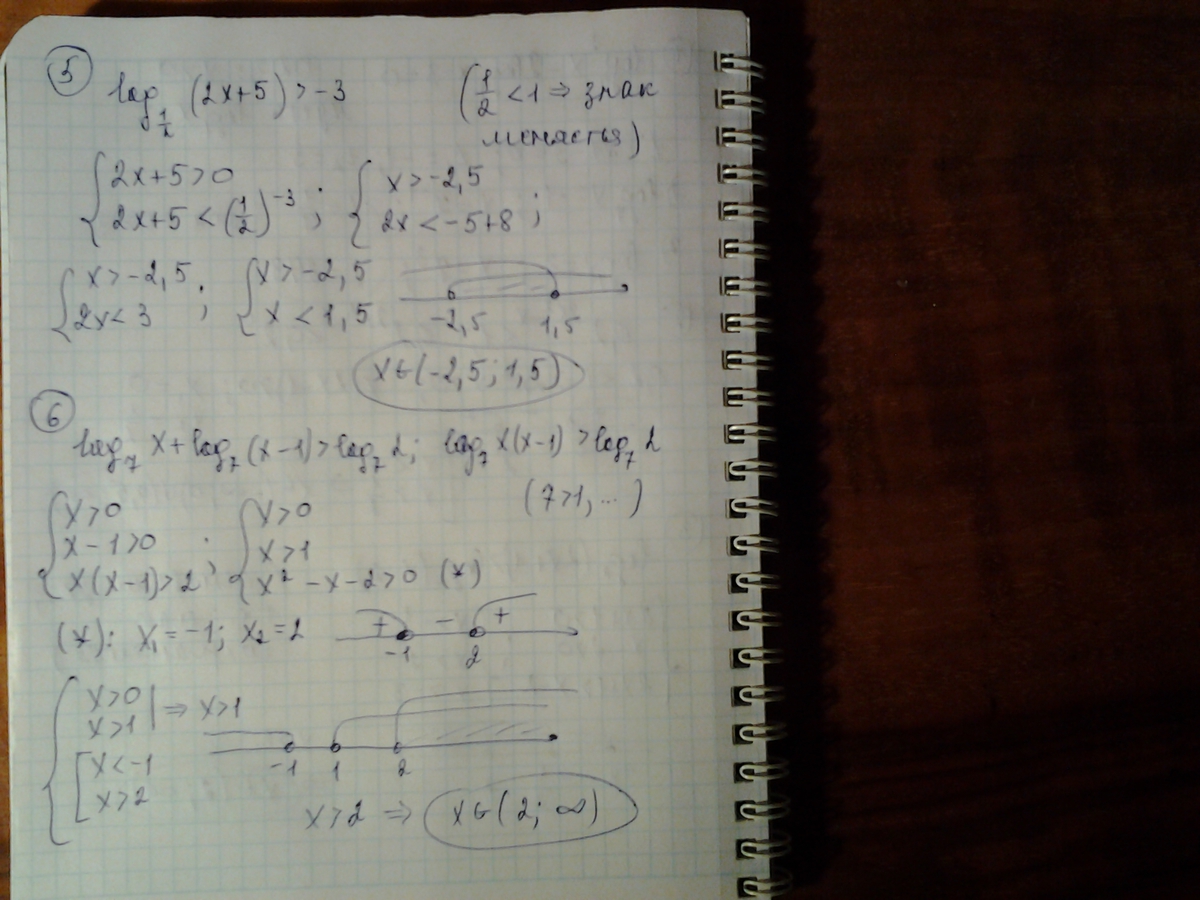
Похожие вопросы
Предмет: Биология,
автор: tttthaha30
Предмет: Биология,
автор: chagina193
Предмет: История,
автор: serikegizekov
Предмет: Физика,
автор: Diana2000r
Предмет: Математика,
автор: Аноним