Предмет: Алгебра,
автор: натусик02
Помогите, очень нужно. Задания на фото. По сложности конец 11, профильный уровень.
Приложения:
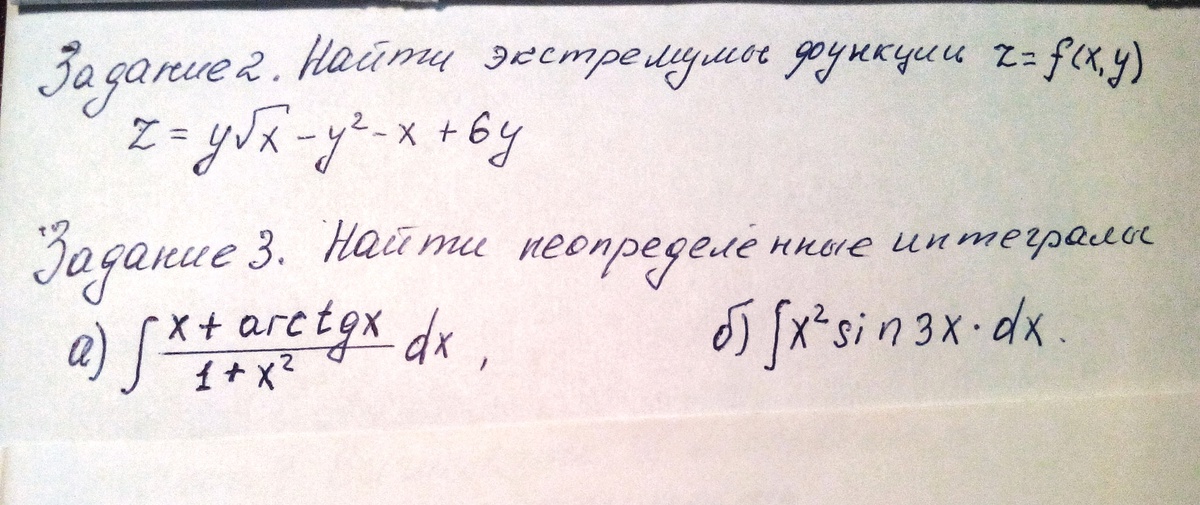
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: bajgazievanazira02
Предмет: Химия,
автор: oxanaosta56
Предмет: Қазақ тiлi,
автор: amiraabayeva
Предмет: История,
автор: 33333alina
Предмет: Математика,
автор: marinadoronina1