Предмет: Алгебра,
автор: ldasha3012
Помогите пожалуйста решить показательное и логарифмическое неравенства.
Приложения:
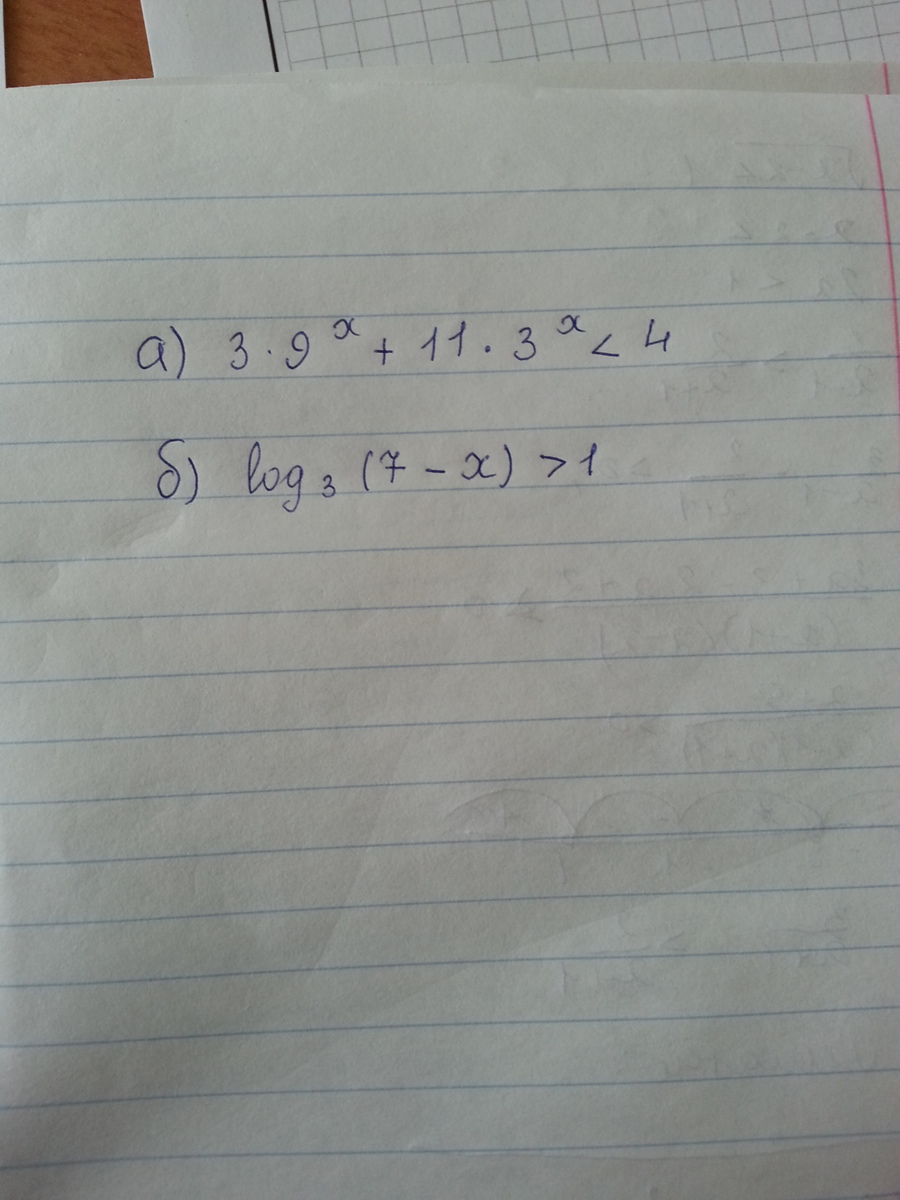
Ответы
Автор ответа:
0
3*3^(2x)+11*3^x<4
3^x=t
3t+11t-4<0
D=121+24
t1=(-11+13)/6=1/3
t2=(-11-13)/6=-4 Быть не может
3^x=1/3
x=-1
Ответ:x принадлежит от (- бесконечности до -1)
2) log3 (7-x)>1
7-x>3
-x>-4
x<4 ОДЗ: 7-x>0 x<7
Ответ: x принадлежит (от - бесконечности до 4)
3^x=t
3t+11t-4<0
D=121+24
t1=(-11+13)/6=1/3
t2=(-11-13)/6=-4 Быть не может
3^x=1/3
x=-1
Ответ:x принадлежит от (- бесконечности до -1)
2) log3 (7-x)>1
7-x>3
-x>-4
x<4 ОДЗ: 7-x>0 x<7
Ответ: x принадлежит (от - бесконечности до 4)
Автор ответа:
0
3*3^(2x)+11*3^x<4
3^x=t, t>0
3t+11t-4<0
(3t-1)(t+4)<0
+ - +
------(-4)-------(1/3)-------
t∈(0,1/3)
0<3^x<1/3
x<-1
2)
3^x=t, t>0
3t+11t-4<0
(3t-1)(t+4)<0
+ - +
------(-4)-------(1/3)-------
t∈(0,1/3)
0<3^x<1/3
x<-1
2)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: redmi2asuper
Предмет: Информатика,
автор: bratan00737
Предмет: История,
автор: asillsharafiden
Предмет: Обществознание,
автор: 89058474556
Предмет: История,
автор: mdna